SVR: 支持向量机在回归问题中的应用

在阅读这篇博客前, 请确保自己对SVM有初步的了解, 如果还不清楚SVM是什么, 可以看下我上篇介绍SVM的博客

回归问题概述

现在有一给定的数据集

T = \{(x_1, y_1), (x_2, y_2), ..., (x_l, y_l)\}

其中

x_i \in \mathbb{R}^n, y_i \in \mathbb{R}

我们要根据数据集, 确定一个在\mathbb{R}^n上的实值函数y=f(x), 来推断将来给出的任意模式x对应的y值

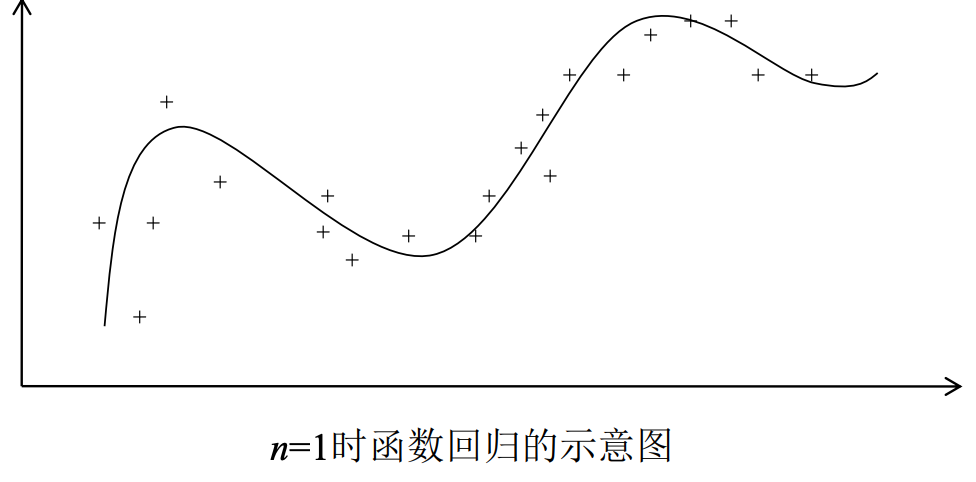
回顾SVM分类

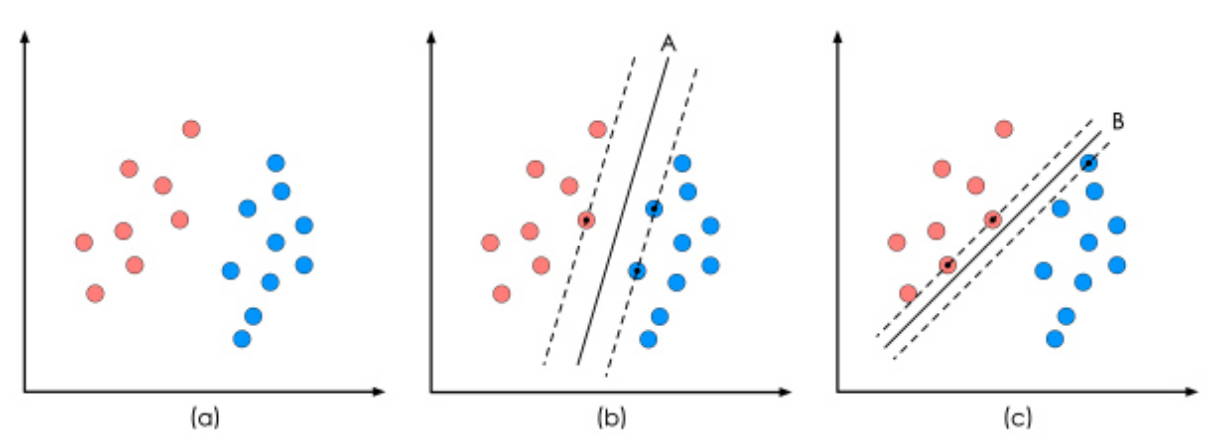
对于一给定的二分类数据集, 我们要确定一个超平面

y = w \cdot x + b

来做出分类, 我们希望离超平面最近的样本点之间距离最大, 这个问题可以表示为

\underset{w, b}{min} \frac{1}{2} ||w||^2 \\
s.t. \, y_i(w \cdot x_i + b) \ge 1, \forall i

不熟悉这个表示的同学, 请去看看开头给出的介绍SVM的博客

回归问题: SVR

在SVR(Support Vector Regression)中, 同样是计算间隔, 不同的是, 我们希望离平面最远的样本点之间间隔最小

• SVM: 离平面最近的点间隔最大
• SVR: 离平面最远的点间隔最小

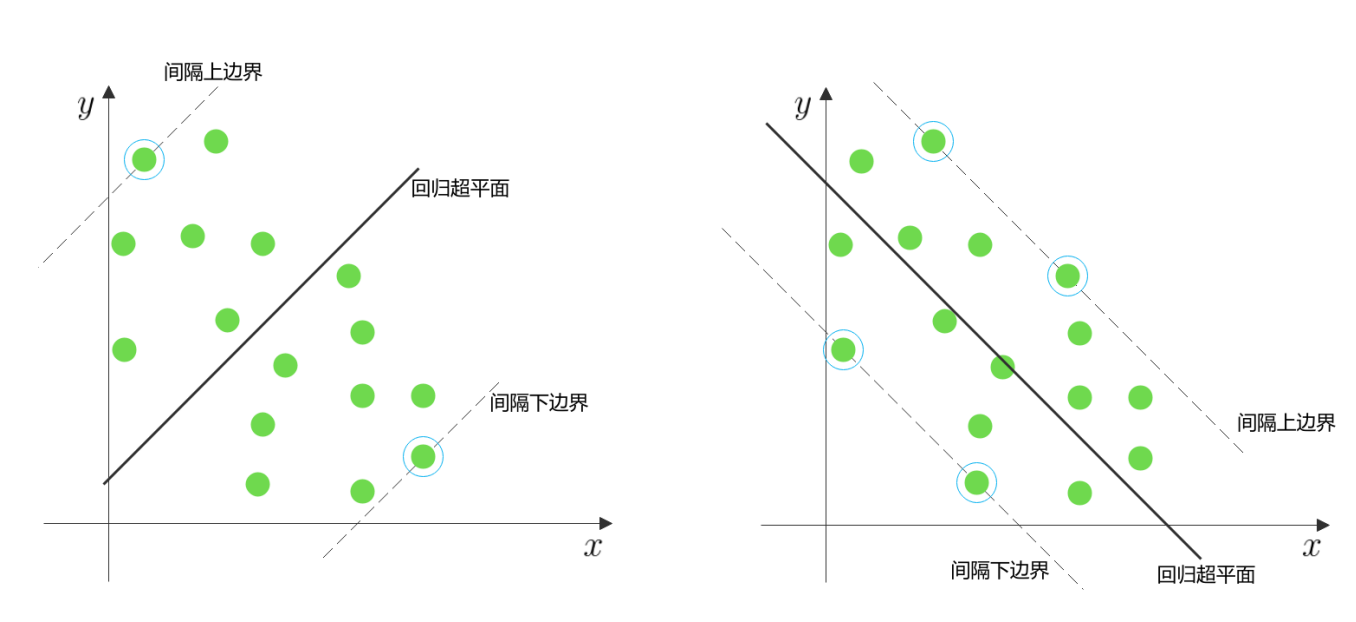
在上图的回归问题中, 显然右图的回归更好一些

相比于SVM的优化目标

\underset{w, b}{min} \frac{1}{2} ||w||^2 \\
s.t. \, y_i(w \cdot x_i + b) \ge 1, \forall i

SVR的优化目标被修改为

\underset{w, b}{min} \frac{1}{2} ||w||^2 \\
s.t. \, |y_i - (w \cdot x_i + b)| \le \varepsilon, \forall i

其中

• \varepsilon是人为设定的参数, 代表允许的最大铅锤误差

在SVM中, 我们希望离平面最近的点间隔最大, 即, 上下临界平面间隔最大, 这个间隔是

d_{svm} = \frac{2}{||w||}

而在SVR中, 我们希望离平面最远的点间隔最小, 即, 上下临界平面间隔最大, 这个间隔是

d_{svm} = \frac{2 \varepsilon}{\sqrt{1+||w||^2}}

落在临界平面上的点, 就被叫做支持向量

在另一方面, ||w||^2作为平面法向量的范数, 其值也代表了平面参数的复杂程度, 最小化他可以控制复杂度, 避免过拟合, 这也可以被看作是一种正则化

进一步推广: 非线形拟合与松弛因子

非线形拟合

为了让我们可以拟合出曲线(面), 我们把目标函数从

y = w \cdot x + b

推广到非线形情况则是

y = w \cdot \varphi(x) + b

为了去除异常数据对结果的影响, 同样的, SVR也可以引入松弛因子

\underset{w, b}{min} \frac{1}{2} ||w||^2 + C \sum_{i=1}^{l} (\xi_i + \xi_i^*)
\\
s.t. \, w \cdot \varphi(x_i) + b - y_i \le \varepsilon + \xi_i, \forall i \\
s.t. \, y_i - w \cdot \varphi(x_i) - b \le \varepsilon + \xi_i^*, \forall i \\
\xi_i, \xi_i^* \ge 0

其中

• \xi_i, \xi_i^*为样本点松弛变量
  • \xi_i是正向超出量
  • \xi_i^*是负向超出量
• C用来平衡宽容度, 越大越严格, 越小越宽容

SVR只对间隔外的样本进行惩罚, 当样本点在间隔内时, 不计算损失