24年12月, 又谈SVM

一年之前写过一篇SVM的博客, 是在学吴恩达的时候, 比较泛泛而谈, 质量不高. 这学期刚好有机器学习这门课, 照例期末抱佛脚, 再重新学一遍SVM, 这次略微接触一些原理, 希望能加深理解.

参考了看了这篇文章你还不懂SVM你就来打我

概述

支持向量机(Support Vector Machine, SVM), 是一种常见的监督学习算法, 经常被用于分类任务, 尤其擅长处理高维数据和小样本数据集.

核心思想

SVM的核心思想是, 对于一组m个d维的数据点, 找出一个最佳决策边界(超平面)将数据分为两个类别

• 在二维空间中, svm会找出一条直线来划分平面中的点

• 在三维空间中, svm会找出一个平面来划分空间中的点

SVM会最大化超平面到不同类的间隔, 以此来避免过拟合, 即, 画出尽可能的粗, 或者厚的超平面

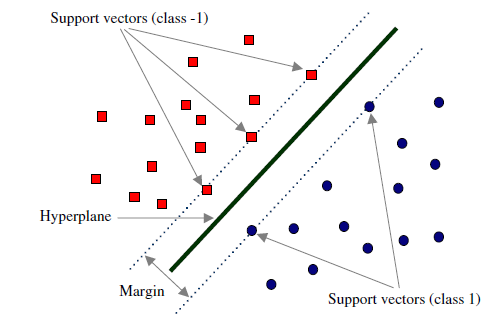
• 最佳的决策边界, 即超平面, 会令距离平面最近的点的距离最大
• 超平面的位置完全由一部分关键样本决定, 这些样本叫做支持向量, 他们是距离超平面最近的点
• 非支持向量对决策边界没有贡献

线性不可分问题

• 如果点在原始空间中线性不可分, SVM可以通过核函数将数据映射到高维空间, 在高维空间中寻找超平面

SVM的数学描述

线性可分的硬边界SVM

线性可分的SVM是最简单的一类问题, 他代表我们的样本在当前空间中可以直接用超平面分开.

此时, 根据是否允许分类错误, 可以分为两类边界

• 硬边界: 不允许分类错误
• 软边界: 引入惩罚项, 允许分类错误

我们先讨论硬边界的情况

假设我们有m组数据:

\{(x_1, y_1), (x_2, y_2), ..., (x_m, y_m)\}

其中x_i \in \mathbb{R}^d是特征向量, y_i \in \{1, -1\}代表正负分类

SVM希望找到一个最佳的超平面:

w \cdot x + b = 0

其中w \in \mathbb{R}^{d}是权重向量, b是偏置, 需要满足以下条件:

y_i(w \cdot x_i + b) \ge 1, \forall i

这是因为

• w \cdot x_i + b是样本点i的决策函数值
• 如果y_i=+1, 则要求w \cdot x_i + b \ge 1, 即正样本必须在超平面正侧
• 如果y_i=-1, 则要求w \cdot x_i + b \le 1, 即负样本必须在超平面负侧

其中支持向量是令等式成立的点, 即满足

y_i(w \cdot x_i + b) = 1

在上述等式两边同时除以$$||w||$$, 根据点到直线的距离公式(广义), 可以得到支持向量到超平面的距离是

\frac{1}{||w||}

不难得到SVM的分类间隔(Margin), 即超平面到两方支持向量的距离和

Margin = \frac{2}{||w||}

SVM希望最大化分类间隔, 也即最小化||w||

在实际情况中, 由于

||w|| = \sqrt{\sum w_i^2}

上面这个形式比较复杂, 我们最优化的目标会是

\underset{w, b}{\text{min}} \frac{1}{2} \|w\|^2

这个最优化是完全等价的,其中

• 超平面的解析式是w \cdot x + b = 0
• w是超平面的法向量
• b是超平面的偏置
• ||w||是超平面的范数, 与间隔大小成反比

简单总结

至此, 我们重新审视上面说过的, SVM会尽可能画出最粗或者最厚的超平面:

超平面的中心平面

w \cdot x + b = 0

超平面的两边界平面

w \cdot x + b = \pm1

这个边界是由支持向量决定的, 代表支持向量的点在边界平面上

上下两边界的距离

{Margin} = \frac{2}{||w||}

是我们最优化(最大化)的目标, 优化约束是

y_i(w \cdot x_i + b) \ge 1, \forall i

这个约束代表, 不仅所有点都要正确预测, 还需要位于上下边界之外, 即

dist \ge \frac{1}{||w||}

这个约束与最优化条件是相辅相成的, 在实际运用中, 我们优化的是等价形式

\underset{w, b}{\text{min}} \, \frac{1}{2} \|w\|^2, \quad 
\text{s.t.} \, y_i (w \cdot x_i + b) \geq 1, \, \forall i

这是一个严格凸优化问题, 他的解是唯一的

求解SVM: 拉格朗日对偶+KKT条件

为了求解下面的问题

\underset{w, b}{\text{min}} \, \frac{1}{2} \|w\|^2, \quad 
\text{s.t.} \, y_i (w \cdot x_i + b) \geq 1, \, \forall i

我们构造拉格朗日函数

L(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{n} \alpha_{i}\left[y_{i}\left(w \cdot x_{i}+b\right)-1\right]

• 引入了拉格朗日乘子\alpha_i \geq 0对应每个约束条件
  • 当约束条件不被满足时, 这一项会通过加法惩罚目标函数
• 目标函数\frac{1}{2} ||w||^2
• 约束y_i(w \cdot x_i + b) \geq 1

为了将原问题转化为对偶问题, 我们将L分别对w和b求导, 并另其为0, 得到优化条件

\frac{\partial L}{\partial w}=w-\sum_{i=1}^{n} \alpha_{i} y_{i} x_{i}=0 \quad \Longrightarrow \quad w=\sum_{i=1}^{n} \alpha_{i} y_{i} x_{i}

\frac{\partial L}{\partial b}=-\sum_{i=1}^{n} \alpha_{i} y_{i}=0 \quad \Longrightarrow \quad \sum_{i=1}^{n} \alpha_{i} y_{i}=0

将上面两个结果带回拉格朗日函数, 消去w和b, 可以得到

L(w, b, \alpha) = \sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i, j=1}^{n} y_{i} y_{j} \alpha_{i} \alpha_{j} \mathbf{x}_{i}^{} \mathbf{x}_{j}

我们的问题现在是

\underset{w, b}{\text{min}} \, \underset{\alpha}{\text{max}} \, L(w, b, \alpha), \quad 
\text{s.t.} \, \alpha_i \geq 0, \, \forall i, \quad 
\sum_{i=1}^n \alpha_i y_i = 0

内层的max是因为

• 最大化\alpha是拉格朗日对偶理论的核心步骤
• 为了确保约束条件被严格遵守, 即, 找到约束的最强形式

外层的min是因为

• 最优化的最终目标: minimize: ||w||^2

因为SVM的原始问题是凸优化问题, 且满足Slater条件, 所以他是强对偶的, 此时

\underset{w, b}{\text{min}} \, \underset{\alpha}{\text{max}} \, L(w, b, \alpha) = \underset{\alpha}{\text{max}} \, \underset{w, b}{\text{min}} \, L(w, b, \alpha)

Slater条件: 在凸优化问题中, 如果Slater条件成立, 则强对偶性成立

KKT条件: 在凸优化问题中, KKT条件是描述一个点是最优解的充要条件

即求解最终的对偶问题

\max _{\alpha} \,  (\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)) \\
s.t. \, \alpha_i \geq 0,  \forall i \\ s.t. \, \sum_{i=1}^n \alpha_i y_i = 0

这个最终的形式是一个标准的凸优化划问题, 我们可以用凸优化的标准形式求解, 比如QP或者SMO

软边界

在上面的情况中, 我们都是用了约束条件

y_i(w \cdot x_i + b) \ge 1, \forall i

这代表所有的点都必须被正确分类, 并且令边界最大. 这在面对一些实际情况的时候并不合适

考虑上图的情况, 如果我们要在当前二维空间画出一条直线, 则不可避免的会产生一些分类错误. 我们现在研究可以容忍错误的情况, 即, 允许模型在一定程度上出错(不满足原约束条件). 这种情况我们称作软边界(Soft Margin)

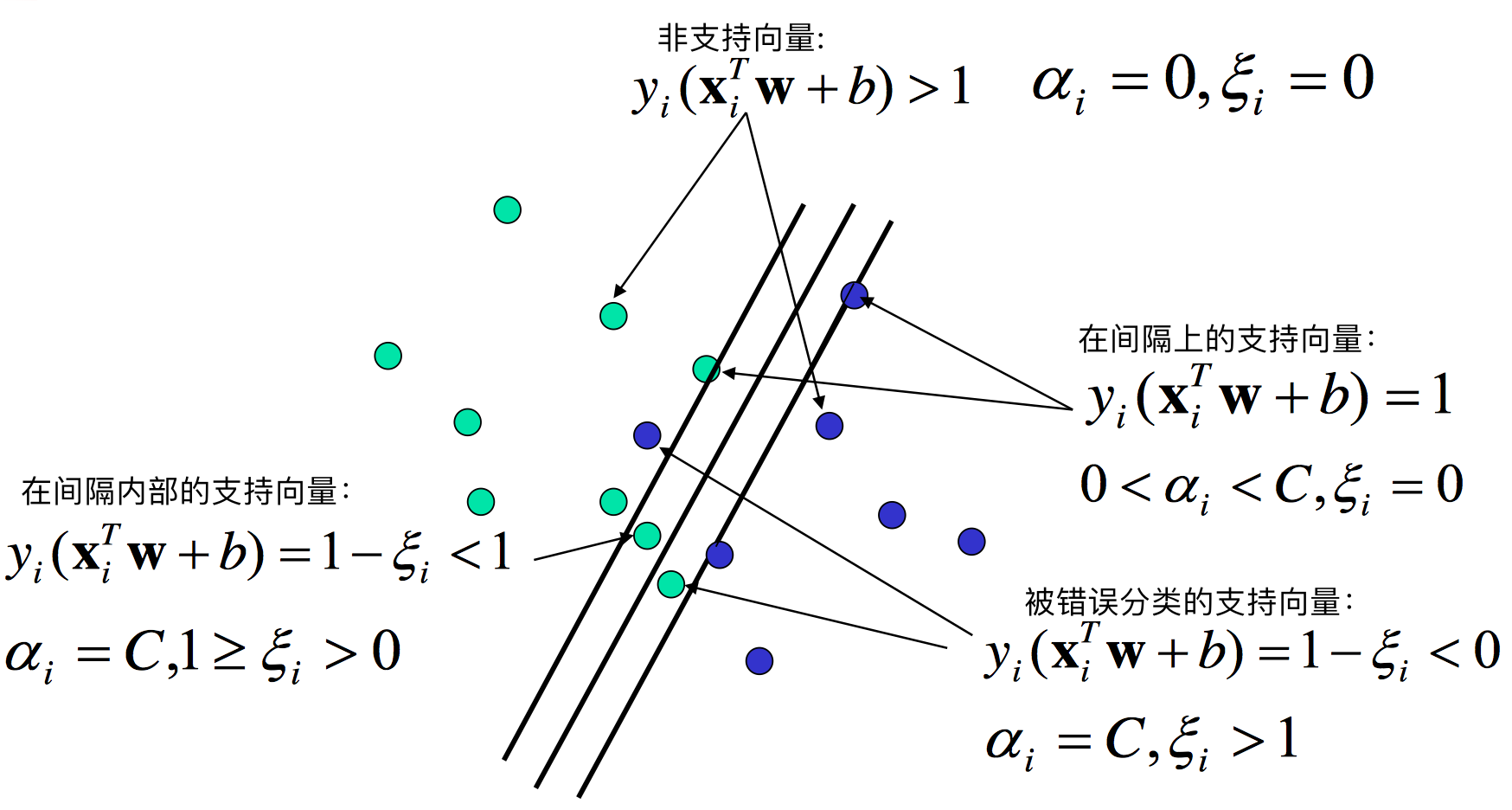
在软边界中, 我们改写目标函数为

\min \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{n} \xi_{i}

约束条件

y_{i}\left(w \cdot x_{i}+b\right) \geq 1-\xi_{i}, \quad \xi_{i} \geq 0

• w是超平面的法向量, b是截距

• \xi_i是松弛变量, 代表i号样本对约束的违反程度

  • \xi_i = max(0, 1-y_i(w \cdot x _ b))
  • \xi_i = 0, 样本被正确分类, 且不在间隔内
  • 0 , 样本被正确分类, 但是在间隔内
  • \xi_i > 1, 样本被错误分类

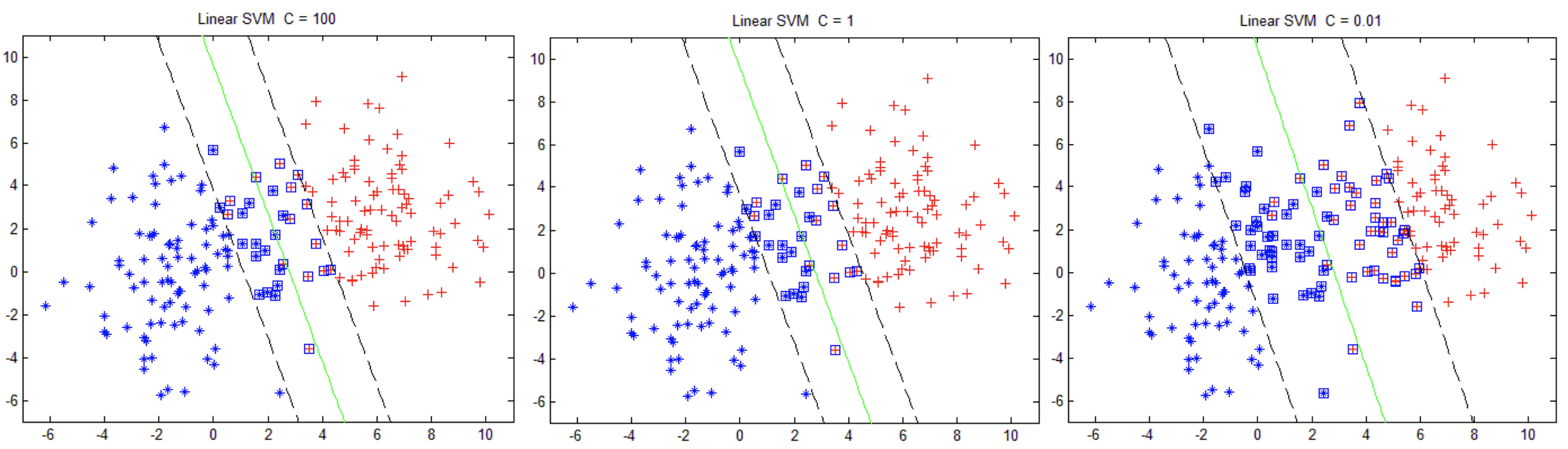
• C是正则化参数, 代表模型对错误的宽容程度

  • C较大时, 模型不容忍错误, 可能过拟合
  • C较小时, 模型允许更多错误, 可能欠拟合

核方法

对于难以在当前空间被线性分割的数据, SVM可以使用核方法来把数据从当前空间映射到更高维度. 这是线性SVM到非线形SVM的推广

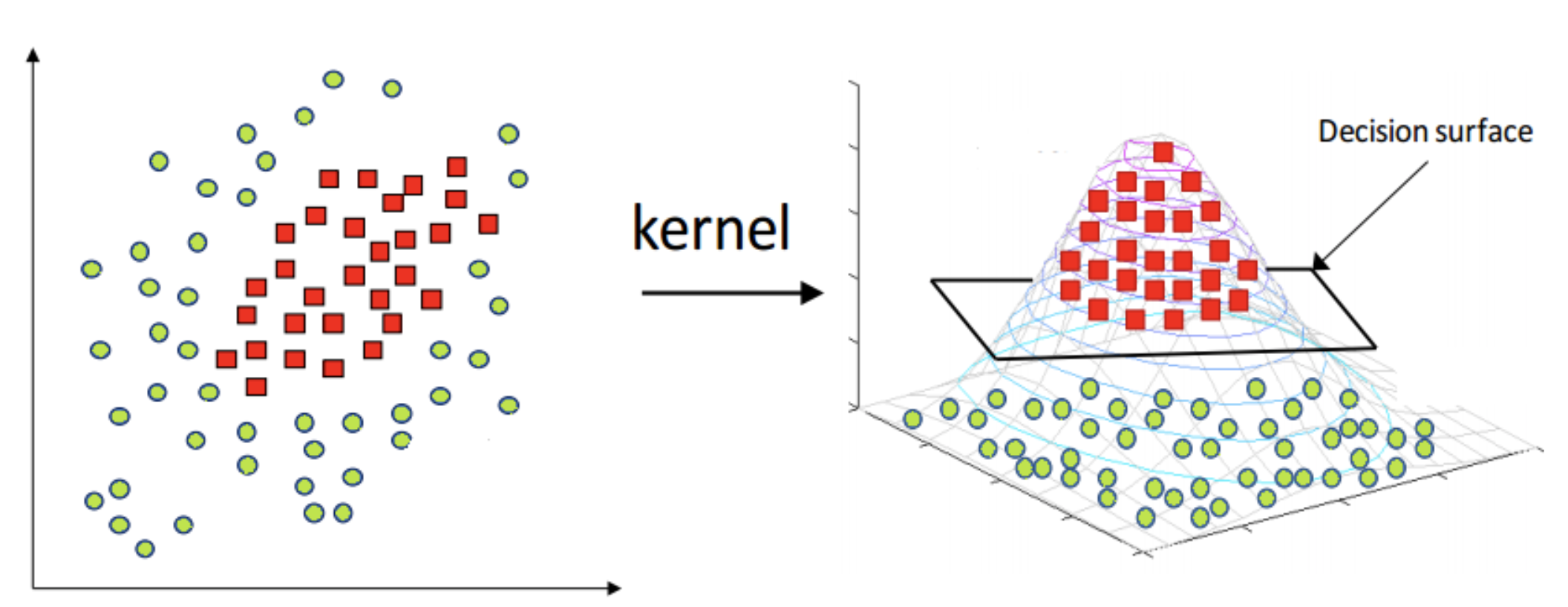
核方法的基本思想是

• 将当前空间内的点映射到更高维度(甚至无穷维)
• 在映射后的高维空间用线性方法学习超平面

核函数

设函数\phi(x)可以将原始数据从低维空间映射到高维空间

x \in \mathbb{R}^{n} \xrightarrow{\phi} \phi(x) \in \mathbb{R}^{m}, m > n

例如, 一个二维平面上的点x=[x_1, x_2]可以映射到三维空间

\phi(x) = [x_1, x_2, x_1^2+x_2^2]

核函数K(x^{(i)}, x^{(j)})用以直接计算高维空间中, 两个数据点的内积

K(x^{(i)}, y^{(j)}) = \phi(x^{(i)}) \cdot \phi(x^{(j)})

核函数直接得到了两点在高维空间的内积, 省略了升维的具体计算, 显著降低了计算复杂性

核函数在SVM中的应用

SVM的优化依赖于样本点之间的内积(比如拉格朗日对偶形式中). 采用核函数代替内积, 则可以令SVM在高维空间进行优化, 并且无需进行显式的高维映射

回顾之前提到的拉格朗日对偶形式:

\max _{\alpha} \,  (\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)) \\
s.t. \, \alpha_i \geq 0,  \forall i \\ s.t. \, \sum_{i=1}^n \alpha_i y_i = 0

经过核函数修正后的拉格朗日对偶形式:

\max _{\alpha} \sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j} K\left(x_{i}, x_{j}\right)

-\alpha_i是拉格朗日乘子

• y_i是标签, 取+1或者-1
• K(x_i,x_j)是核函数, 表示在高维空间中计算 \phi(x_i) 和\phi(x_j) 的内积

常见的核函数

线性核

K(x_i, x_j) = x_i \cdot x_j

• 等价于不向高维映射

多项式核

K(x_i, x_j) = (x_i \cdot x_j + c)^{d}

• 适用于具有多项式关系的非线性数据

高斯核

K\left(x_{i}, x_{j}\right)=\exp \left(-\frac{\left\|x_{i}-x_{j}\right\|^{2}}{2 \sigma^{2}}\right)

• 是最常用的核函数, 适合处理任意分布的非线性数据。

• 能够将数据映射到无限维的特征空间

Sigmoid核

K\left(x_{i}, x_{j}\right)=\tanh \left(\beta x_{i} \cdot x_{j}+c\right)