说在前面:既然是没什么包装的模板题,那么建议大家打细致一些,如果不很清楚,代码量多一些也没关系,一条一条重在理解透彻
好,进入正题:
很明显的一道Tarjan,题解中讲Tarjan的神犇也有很多,但是我自认为还可以多用些图和Markdown将这个算法讲的更清楚些,所以这里重新讲一下Tarjan:
这里普及基本概念:
- 强连通分量:对于图G来说的一个子图中,任意两个点都可以彼此到达,这个子图就被称为图G的连通分量(一个点就是最小的连通分量)
- 时间戳:搜索到一个点时,这个点将被赋予一个 唯一 的时间量,并且越早搜到的点时间戳越小(当然了)
Tarjan是一个基于深搜,可以求解图中强连通分量的的算法,基本思想请看图:
在我们对一个图进行深度优先搜索时,走过的边会得到一棵搜索树,搜索树可以看做是原图抛弃了一些边而形成的
这便是一棵搜索树了
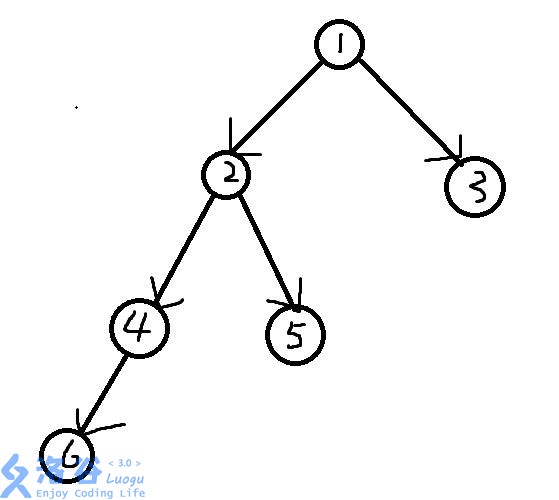
我们对抛弃掉的边做一个分类,对于这棵树中被还原的原图中的边有三种:
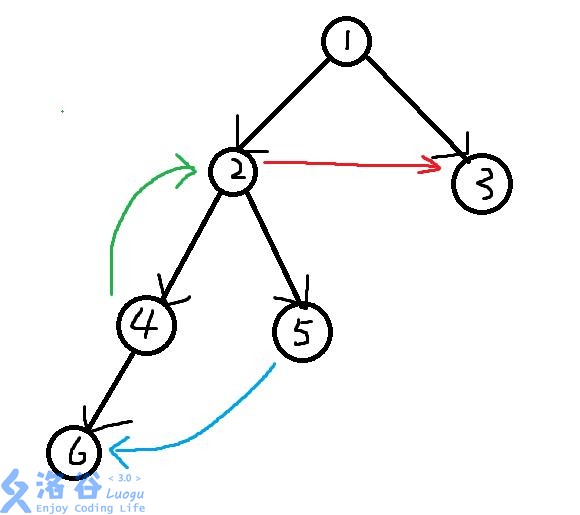
- 红色的边-横叉边
- 蓝色的边-前向边
- 绿色的边-后向边
不难发现,横叉边和前向边都无法构成回路,即不能形成大于一个点的强连通分量,所以我们要做的,就是找出重要的后向边来
怎么找后向边呢?你可以回想一下刚才提到的“时间戳”,没错,如果我们搜索到了一个之前搜过的点,且他当前点的祖先一样,那么毫无疑问的,我们走在了后向边上
Tarjan算法使用两个数组来维护这个信息:
- dfn[maxn]:储存每个点的时间戳
- low[maxn]:储存每个点访问祖先的能力
什么是访问祖先的能力呢?就是说,这个点最多能走回头路到什么地步,low数组储存的是他能访问到的最早祖先的dfn值,如果这个点没有回头路可走,那low值就是他自己的dfn值咯
好了,说了这么多,相信你已经有一些感觉了,我们来看Tarjan的模板代码:
struct edge{
int x,y,w;
}E[maxm];
int dfn[maxn],low[maxn],tmmk=0;
bool v[maxn];//v数组用来跟踪这个点是否已经处理完毕,我们稍后会见到它的用法
stack<int> S;
void tarjan(int x)
{
dfn[x]=low[x]=++tmmk;//每个点在最开始被访问时,时间戳和low值都是一样的
S.push(x);
v[x]=true;
for(int i=head[x];i;i=next[i])//链式前向星查邻接点
{
int y=E[i].y;//不熟悉的同学请像这样打多一点,有助于理解
if(!dfn[y])//dfn的初值都是0,如果这个点没有搜过,就递归搜索
{
tarjan(y);
low[x]=min(low[x],low[y]);//此时搜索已经回溯,我们可以确定y的low值已经更正,所以用它来更新x的
}//因为y在x的后面,所以y能访问到的祖先x一定可以访问到
else
if(v[y])//如果y点搜过了且在栈里,说明我们找到了 后!向!边!
low[x]=min(low[x],dfn[y]);
}//但是此时我们还不能急着处理,为什么?因为有回溯到根了以后我们在收集到了完整的信息
if(dfn[x]==low[x])
{//dfn和low一样,你就是与众不同的根节点
ans++;//ans是强连通分量的个数
int y;
do{
y=S.top();
S.pop();
v[y]=false;
col[y]=ans;//y点属于编号为ans的强连通分量
g[ans].push_back(y);//存下每个强连通分量的成员
}while(y!=x)//在这里将栈里的点全部倒出来(倒垃圾一样..)
}
}回到题目!
题目要求求出图中最大强连通分量,和其中所有的点
我们可以看出,以上模板中col数组用不着了,存成员还是必要的,但是要求字典序输出,这个向量就不很方便了,我们可以用优先队列解决这个问题
关于优先队列的基本用法可以看我博客,这里关系不很大不做深究qwq
AC代码:不开O2 55ms(偷懒用stl的代价)开O2 35ms
#include<bits/stdc++.h>
using namespace std;
const int maxn=6000,maxm=110000;
int n,m;
int read(){
int x=0;char c=getchar();
while(c<'0' || c>'9')c=getchar();
while(c>='0' && c<='9'){
x=(x<<3)+(x<<1)+(c^'0');
c=getchar();
}
return x;
}
int head[maxn],nxt[maxm],id=0;
struct edge{
int x,y;
}G[maxm];
void add(int x,int y){
G[++id].x=x;
G[id].y=y;
nxt[id]=head[x];
head[x]=id;
}
struct pointer{//这是一个指针,p指向连通集编号,siz是他的大小方便排序
int p,siz=0;
int diction;//diction是第一个点的编号,如果严格字典序请改成数组
}p[maxn];
int dfn[maxn],low[maxn],col[maxn],
tmmk=0,cnt=0;
stack<int> S;
priority_queue<int,vector<int>,greater<int> > g[maxn];
bool instk[maxn];
void tarjan(int x){
dfn[x]=low[x]=++tmmk;
S.push(x);
instk[x]=true;
for(int i=head[x];i;i=nxt[i]){
int y=G[i].y;
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
}
else if(instk[y])
low[x]=min(low[x],dfn[y]);
}
if(dfn[x]==low[x]){
cnt++;
int y;
p[cnt].diction=S.top();
do{
y=S.top();
S.pop();
instk[y]=false;
col[y]=cnt;
p[cnt].p=cnt;
p[cnt].siz++;
g[cnt].push(y);
}while(y!=x);
}
}
bool cmp(pointer a,pointer b){
if(a.siz!=b.siz)
return a.siz>b.siz;
else
return a.diction<b.diction;
}
int main(){
n=read(),m=read();
int x,y,f;
for(int i=1;i<=m;i++){
x=read(),y=read(),f=read();
add(x,y);
if(f==2)
add(y,x);
}
memset(dfn,0,sizeof(dfn));
memset(instk,false,sizeof(instk));
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i);
sort(p+1,p+cnt+1,cmp);
printf("%d\n",p[1].siz);
while(!g[p[1].p].empty()){
printf("%d ",g[p[1].p].top());
g[p[1].p].pop();
}
return 0;
}
PS:本题数据略水,题解中有些并没有考虑到一般字典序还A掉的,希望同学们注意。另:我这样做也只考虑第一个数的字典序,如果严格排列把字典diction改成数组即可
PSPS:大半夜写这个挺累的,如果有帮到你,请不要吝惜你的赞(笑)
