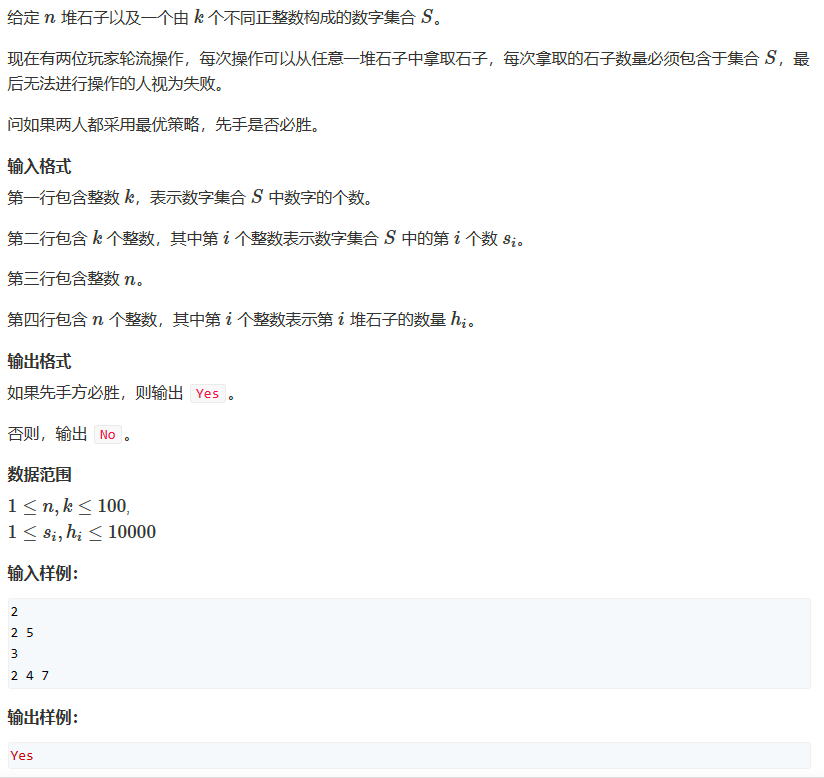
SG函数是解决博弈论问题的利器
在正式解题之前首先需要了解以下知识:
有向图游戏
给定一个有向无环图,图中有一个唯一的起点,在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动,每次可以移动一步,无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏(ICG)都可以转化为有向图游戏。具体方法是,把每个局面看成图中的一个节点,并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。
介绍上述的有向图游戏是为了引入下面两条概念
mex运算
mex运算是对一个自然数集的运算,返回不属于该集合的最小自然数
例如对于集合G={0,1,2,4},$$mex$$(G)的结果是3
SG函数
SG函数是一个自变量为游戏状态(在有向无环图中是一个节点),返回值为自然数的特殊函数
对于一个公平组合游戏对应的有向无环图,我们规定游戏终点的SG值为0,并且对于其中任何一个非终点的节点x有
sg(x) = mex\{sg(y_1), sg(y_2),sg(y_3), \cdot \cdot \cdot ,sg(y_n)\}其中y是x的所有后继节点
可以举一个例子,图中黑色数字是点的编号,蓝色数字是SG值:
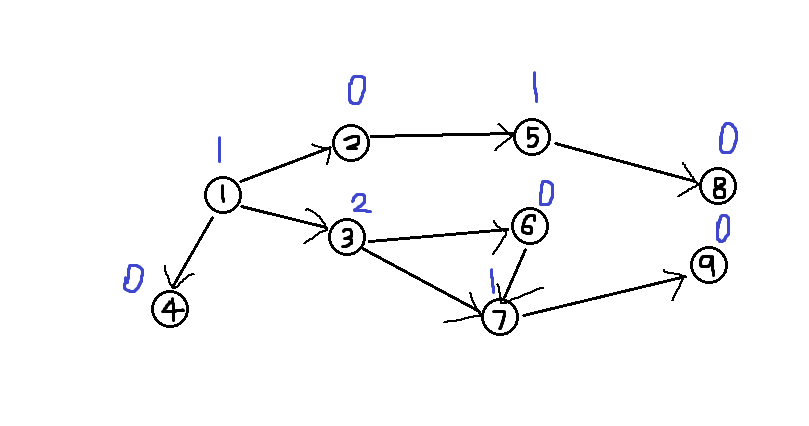
首先4,8, 9号点作为终点SG值是0,而5, 7号点只有通向终点的一个后继,SG值为1 6号点只能通向SG值为1的7号点,所以SG(6) = 0 三点可以通向SG值分别为0,1的6,7号点,SG(3)=2
以此类推可以写出所有点的SG值
定理:有向图游戏的某个局面必胜,当且仅当该局面对应节点的SG函数值大于0。
证明方法和经典NIM游戏一样,可以证明:
- 游戏终点(必败局面)的SG值为0
- 任何一个SG值不为0的点,我们都可以通过一次操作使其走到一个SG值为0的点
- 当处在一个SG为0的点时,无论如何操作都不能走到下一个SG值为0的点
而对于多个有向图的游戏(在本例中具体为多堆石子),有定理:
由n个有向图组成的游戏的某个局面必胜,当且仅当该游戏所有起点的SG值异或和不为0
这一定理被称作Sprague-Grundy定理
这里有一篇CSDN的证明,思路和上述证明方法相似 
讲完这些终于可以看本题了
本题可以抽象为有向图游戏,将每堆石子抽象为一个图,状态就是石子存量
因为可以选取的方法固定, 所以对于每个状态的SG值都是固定的(这一步有些难想:为什么状态信息只需要石子存量?)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 10100, K = 200;
int s[K], f[N];
// s是所有可供选择的取法集合, f是对一个状态的sg值, 这里的一个状态具体来讲是石子的余量
// 需要注意的是,石子余量和操作次数,轮到谁操作都没有关系,和状态的出现位置等等也没有关系
// 将本例抽象成有向无环图之后, 状态信息只有石子存量, 每堆石子都是一个独立的图
// sg(x)中的x就是石子存量
int n, k;
// 本例中求取sg值的方法是记忆化搜索
int sg(int x)
{
if(f[x] != -1)
return f[x];
unordered_set<int> T; // T是x点后继点的sg值集合
for(int i = 1; i <= k; i++)
{
int d = s[i]; // 可选集合的第i个选项:拿d个
if(x >= d)
{
// 如果可以拿就把后继节点的sg值加入集合
// 这样看来应该是后序遍历
T.insert(sg(x - d));
}
}
// 求sg值的部分
// 一个点的SG值是最小不属于后继点SG值的自然数
// 如果他本身是终点,SG值就是0
for(int i = 0; ; i++)
if(!T.count(i))
return f[x] = i; // 记忆化不能忘了,直接return i就飞了
}
int main()
{
// ios::sync_with_stdio(false);
cin >> k;
for(int i = 1; i <= k; i++)
cin >> s[i];
int res = 0;
cin >> n;
memset(f, -1, sizeof f);
for(int i = 1; i <= n; i++)
{
int x;
cin >> x;
res ^= sg(x); // 多个有向图游戏必胜当且仅当所有起点SG值异或和不为0
}
if(res)
puts("Yes");
else
puts("No");
return 0;
}