合并果子(Huffman树模板)

合并果子问题可以抽象成如下模型： 对于一个数集s，求一个完全二叉树树，以集合中的元素作为叶节点，使得该树叶节点的带权路径和最小，这种树就是Huffman树

带权路径和计算公式如下

\sum_{i=1}^{n} w_id_i

其中wi是叶节点的权值，di是深度

例如下图是一颗Huffman树 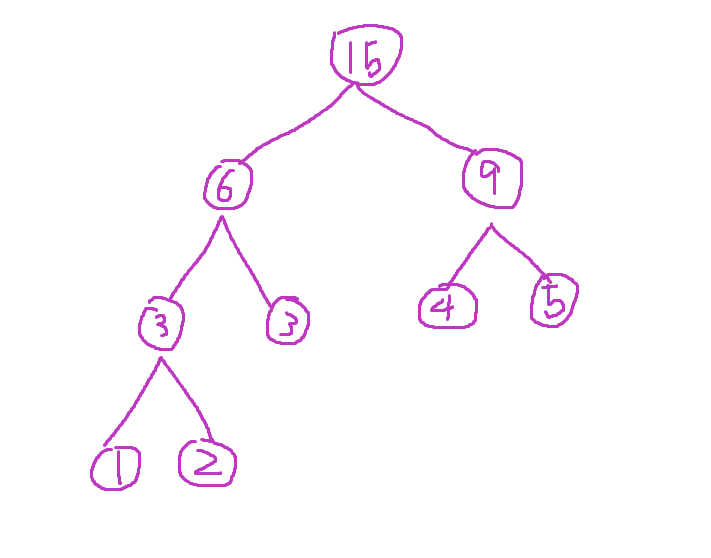其叶节点有5个：1,2,3,4,5，且总权值为33

不难看出Huffman树的构造是一个贪心问题，因为位置越深的节点需要乘以越大的深度d，所以我们希望他的权值尽量的小

权值越小的点越靠下是Huffman树的核心思想

合并果子这题是Huffman数的模板，Huffman树的实现可以直接用小根堆，每次弹出两个堆顶元素，合并后再插入堆中即可

#include <bits/stdc++.h>

using namespace std;

int main() {
    int n;
    cin >> n;
    priority_queue<int, vector<int>, greater<int>> Q;

    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        Q.push(x);
    }

    int res = 0;
    while(Q.size() != 1) {
        int a = Q.top();
        Q.pop();
        int b = Q.top();
        Q.pop();
        Q.push(a + b);
        res += a + b;
    }

    cout << res << endl;

    return 0;
}