在本节中我们希望通过拟合一个线性函数，对一个实际问题进行线性回归
单变量线性回归
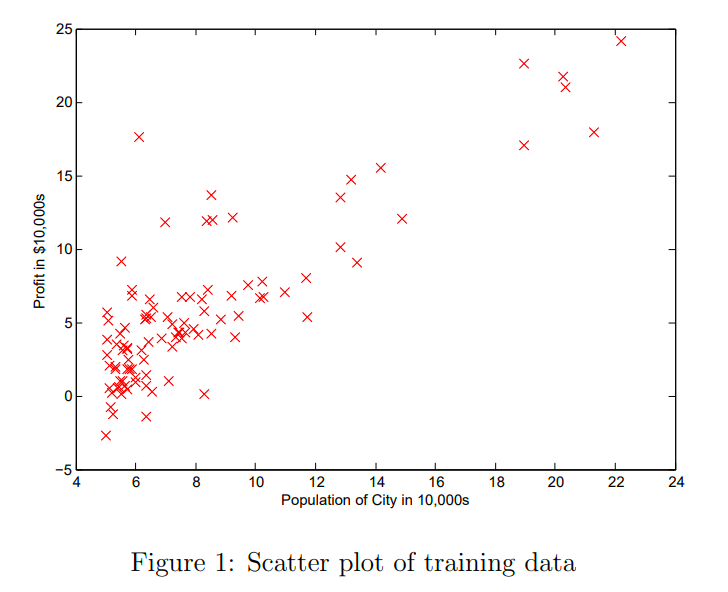
想象我们作为一家连锁商店的CEO，上图是一个所有店面的所在城市人口-利润分部图，我们希望拟合一条直线，来衡量城市人口与利润的关系，以便来决定下一家店面开在哪里
这是我们希望拟合的直线方程
h(x) = \theta ^T X = \theta _0 + \theta _1 x h代表预测(hypothesis)，当我们用
x^{(i)}, y^{(i)}来表示数据集中的每个点时，我们规定损失函数
J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}}即估计数据与实际数据的均方差，我们当前的问题是，找到两个θ，令J(θ)最小，即可拟合出一条合适的直线，使得他离每个点平均距离最近
这里的2m可以看做是方便后续计算而多写了一个2，因为损失函数总会对某个变量求导，而恰好可以与平方项的求导结果抵消
损失函数J的自变量是θ，在本例中有两个，所以可以想象在如下的一个函数中，找寻平面的最低点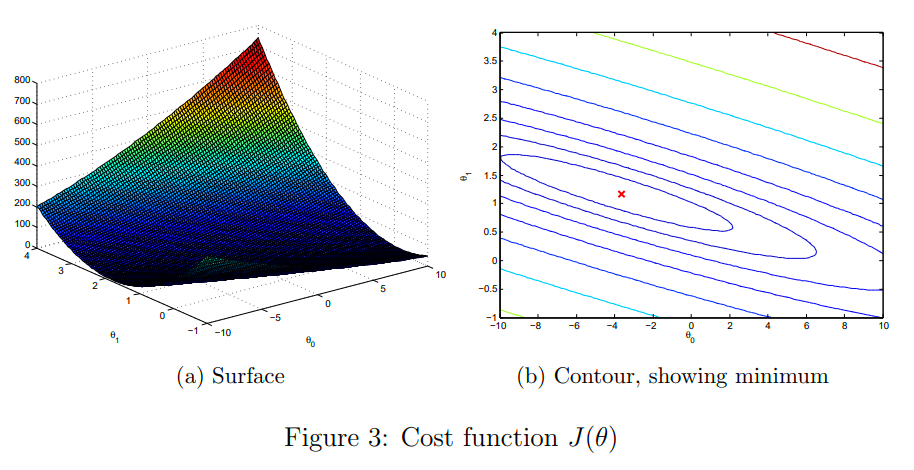 
如何找寻呢？梯度下降的方法是对于第一次计算损失，我们可以任选两个θ值，此时我们可以找到上图平面的一点，通过计算梯度，来衡量下一次迭代的方向，然后向该方向前进一小步
{{\theta }_{j}}:={{\theta }_{j}}-\alpha \frac{\partial }{\partial {{\theta }_{j}}}J\left( \theta \right)其中alpha称为学习率，可以影响每一步的步长
事实上:
\frac{\partial }{\partial {{\theta }_{j}}}J\left( \theta \right) =
\frac {1}{2m} \frac{\partial }{\partial {{\theta }_{j}}}\sum_{i=1}^{m} h_\theta (x^{(i)})-y^{(i)})^2
其中
h_\theta (x^{(i)})=\theta_0+\theta_1x所以
{{\theta }_{j}}:={{\theta }_{j}}-\frac{\alpha}{m} \sum_{i=1}^{m} (h_\theta (x^{(i)}-y^{(i)})x_j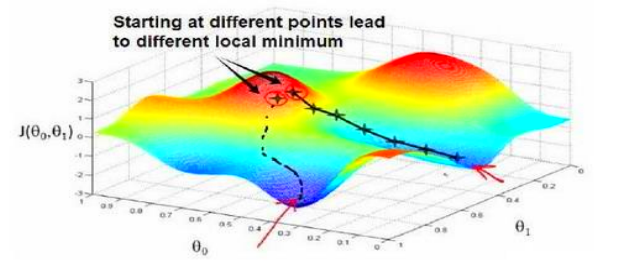
上图说明了一个问题，在损失函数比较复杂时，梯度下降算法只能找到一些局部的最小值，不能保证一次走到全局的最小值
在本例中，损失函数很简单，最小值是唯一的，所以梯度下降算法必可以一次找到最优的θ
多变量线性回归
想象一个问题，在刚刚的例子中，我们得知的信息不单单只有城市人口与利润，还有诸多影响因素，比如营业时间，员工素质，…假设我们已经可以很好的用数值来衡量这些因素，我们可以认为利润是这些因素共同作用的结果
{{h}_{\theta }}\left( x \right)={{\theta }^{T}}X={{\theta }_{0}}{{x}_{0}}+{{\theta }_{1}}{{x}_{1}}+{{\theta }_{2}}{{x}_{2}}+...+{{\theta }_{n}}{{x}_{n}}当然，我们还是假设每个因素对利润的结果都是线性（一次）的
此时用矩阵（向量）的角度来讨论这个问题会方便的多
此时，X的每一行是一组数据，代表数个变量，总共有m组
此时的损失函数与迭代方法不变