逻辑回归(logistic regression)是应用广泛的一种分类算法
需要注意的是,逻辑回归和“回归”没什么关系,尽管他的名字里有这个词
分类问题
在分类问题中,我们需要预测的目标不再是回归问题中连续的值,而是离散的
比如判定一个邮件是否是垃圾邮件,一个肿瘤是否为恶性,都是二元分类问题
当然分类问题也可以是多元的,比如MBTI16人格测试
现在我们以判定肿瘤是否为恶性为例,假设我们有一组训练集,包含肿瘤的大小和是否为恶性两个信息,显然我们的预测算法应该是接受一个变量(大小)输出一个变量(是否为恶性的)
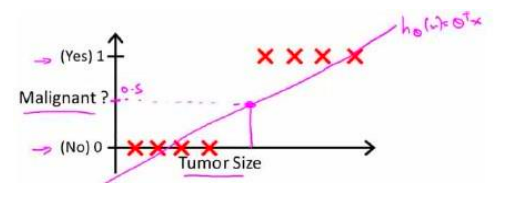
我们很自然的可以想到运用上节说到的线性回归来尝试解决这个问题,对于若干肿瘤(图中的红叉),可以拟合出一条直线来预测结果,例如,y大于0.5时候预测1,否则预测0
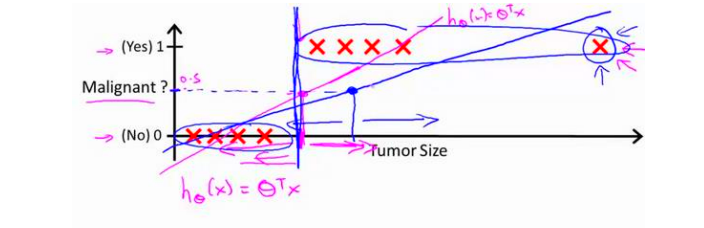
这个做法带来了一个问题,如图右边的一个非常大的恶性肿瘤(很符合实际),他的出现会令原先拟合出的直线变得平坦。观察粉色直线受到的影响,而这会影响模型认为的恶性肿瘤阈值,这里是变大了
这足以说明线性回归不适用于解决分类问题
此时我们引入逻辑回归来解决图中的问题,逻辑回归的函数即将线性回归函数外面包一层sigmoid函数来实现

在逻辑回归中,我们认为函数输出(h(x))是对于给定的变量x,x由参数theta影响,该样本属于1分类的概率,即
h_{\theta}(x) = P(y = 1|x; \theta)本例中是肿瘤是恶性的概率
决策边界
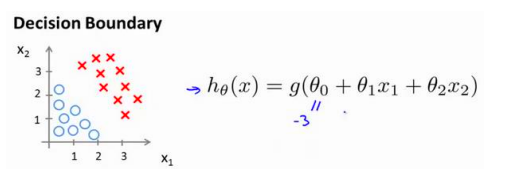
假设我们现在在进行一个双变量的二元逻辑回归,图中给出了两种类别的数据和预测函数,我们暂时不谈theta向量的更新方式,假设他已经更新好了,即:(-3, 1, 1)
此时当x1+x2>3时,模型会预测1,否则预测0,这里的x1+x2=3直线就叫做决策边界(Decision Boundary)
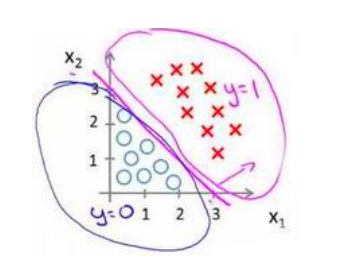
决策边界可以非常复杂,这取决于参数列表长度(变量的幂次),比如上图中显然只支持直线边界,当我们延长参数列表至x1x2平方时,可以支持曲线边界

代价函数与梯度下降
我们如何来衡量一次拟合的效果?如果使用上节的均方差损失函数:
J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}}会出现问题,因为h(x)不再试线性的,他的解析式非常复杂,同样的,他的均方差损失函数也不是凸函数
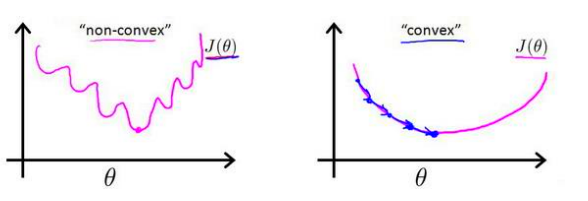
很多局部最小值会影响梯度下降的结果
事实上,逻辑回归经常用到以下损失函数:
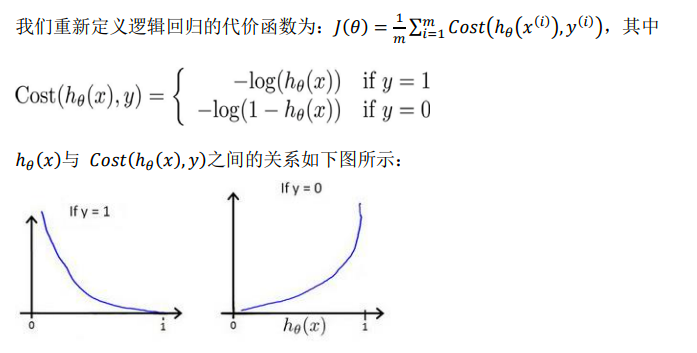
观察图像可以发现,当y=1时,预测值离1越远,代价越趋近无穷,y=0时亦然。而当预测正确时,代价为0
事实上上述函数可以写成如下比较紧凑的形式
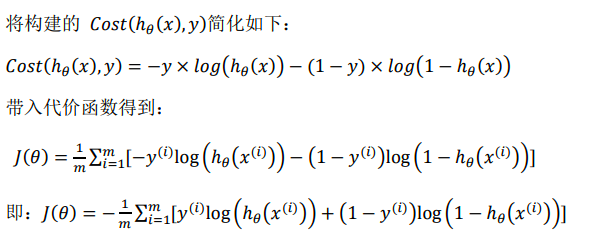
这个损失函数是凸的,即没有局部最小值,非常适合梯度下降

其中J(theta)求导的过程放在博客最后
可以发现参数迭代方程和均方差迭代方式完全一样,这是否说明逻辑回归和线性回归在梯度下降方面没有区别呢?答案是否定的,虽然迭代表达式相同,但是h(x)的表达式不同,事实上,逻辑回归的h(x)比线性回归多了一层sigmoid函数
多分类
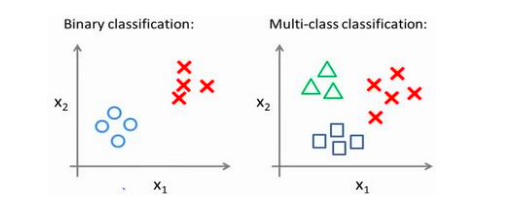
如果问题变成了多个类别分类,我们仍可以用上述方法来解决——即,用“一对余”方法
对于每个分类,我们都生成一个分类器,来判定“是否为该分类”问题,图中的三种类别,就需要三个不同的分类器

在预测时,我们会依次运行三个分类器,然后选出可能性最大的一个结果作为最终结果
