过拟合问题
考虑这样的一个回归问题,对图中红色叉数据拟合出函数来预测结果
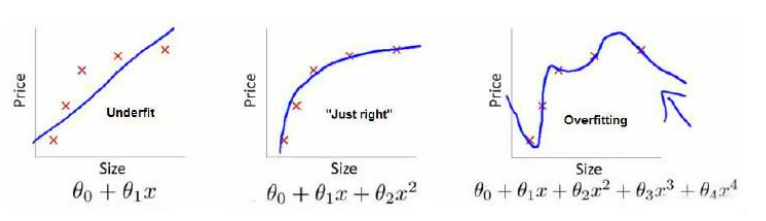
从左到右选用了一次增多的参数数量,可以看到左图因为参数过少,无论如何拟合都不能让人满意
中图可以看做一个比较好的拟合结果
右图就比较有意思,他的参数量过多了,这会带来一个问题:拟合效果确实更好了,即,从损失函数的值来看,确实比中图还高,但这并不是好的拟合结果,因为函数过于执着的符合数据集中的数据,而没有达到我们真正的目的:预测。这种情况就叫过拟合,而左图的情况叫欠拟合。
过拟合在分类问题中也会出现,比如逻辑回归:
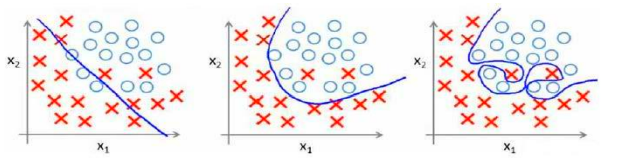
要避免过拟合问题可以减少参数量或者正则化
减少参数量可以人工减少,也可以用一些算法来做,但是这会导致一些信息的丢失,我们这里讨论正则化的方法
正则化
正则化保留所有的参数,但是希望参数尽可能的小些
比如上述回归问题中,我们的模型如下 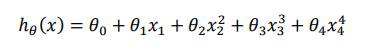
我们知道,高阶的x项系数会显著影响函数图像的曲折程度,所以我们可以在代价函数中加入惩罚项,来限制高阶x项系数的大小,比如这样
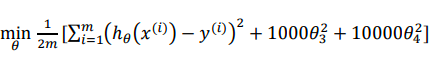
这会使得theta3,4在变大时,模型会受到惩罚,从而限制他们的大小
用这个代价函数训练的结果大致如下:
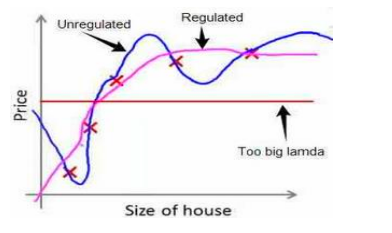
但是在实际问题中,我们不知道哪些参数是我们要惩罚的,所以我们会对所有参数都进行惩罚,并且用代价函数最优化算法来选择每个参数的惩罚力度,通常会写成这种形式
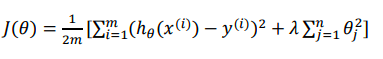
注意,按照惯例,我们不惩罚theta0,即和x0 = 1对应的参数
如果我们过度的增大惩罚参数,即,lambda的值过大,就会造成上图中红线的情况,算法发现无论选择什么参数都会受到严重的惩罚,所以将所有参数都置零,这样的损失函数值甚至低于正确的拟合结果
正则化线性回归
修改后的线性回归代价函数如下: 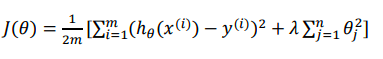
在梯度下降时,需要注意我们不对theta0正则化,所以要分类讨论

可以看出,正则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的 基础上令𝜃值减少了一个额外的值
正则化逻辑回归
修改后的逻辑回归代价函数如下:
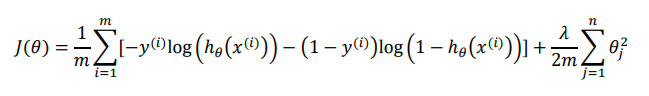
梯度下降公式:
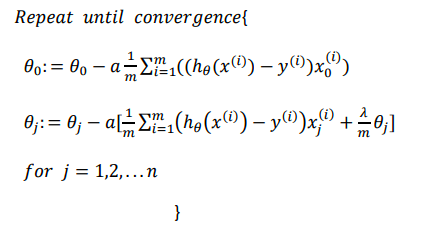
仍需注意,虽然梯度下降公式看起来和线性回归一样,但是两者因为h(x)的含义不同,本质上并不相同
