偏斜类(Skewed class)
偏斜类指训练集中有非常多同一类的实例,举个例子:
如果我们将一家医院的肿瘤检测数据作为数据集, 可能大部分数据都不是恶行肿瘤(癌症), 比如说, 医院数据中只有0.5%的恶性肿瘤
如果我们用这些数据训练出一个模型, 这个模型只会做出一个动作: 判断肿瘤为非恶性. 这显然不是一个好模型, 但是他仍有99%的概率会对一个未知情况的病人做出正确的判断
显然我们之前的衡量模型表现的指标不够完善, 下面给出新的指标
查准率(Precision)与查全率(Recall)
我们将算法预测的结果分为四种情况:
- 正确肯定(TP): 预测真, 实际真
- 正确否定(TN): 预测假, 实际假
- 错误肯定(FP): 预测真, 实际假
- 错误否定(FN): 预测假, 实际真
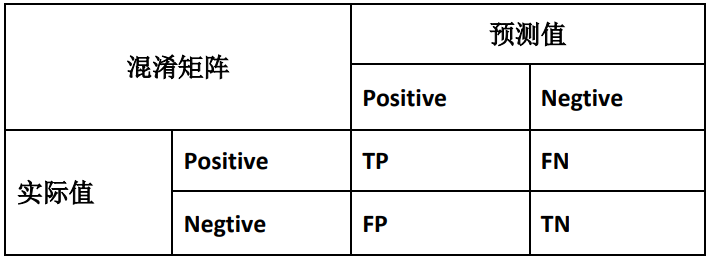
则:
precision = \frac{TP}{TP+FP} \\
recall = \frac{TP}{TP + FN}recall也叫召回率, 可以如此形象的理解, 即将所有样本放归自然后, 算法再次找出的概率
precision是在我们预测有肿瘤的人中, 确实有肿瘤的占比 recall是所有确实有肿瘤的人中, 我们成功预测有肿瘤的占比
这样以来, 上述的算法recall是0, 反应了他在这方面表现很差
查准率与查全率的权衡
在偏斜类的实际应用中, 我们希望平衡precision和recall, 来确保算法表现不过于保守, 或者激进
假设我们用逻辑回归解决上面的问题, 并且用0.5作为真假阈值

如果我们想趋于保守, 只在非常自信时给出恶性肿瘤的结果, 可以设置比0.5更大的阈值, 这样做会提高precision
如果我们想趋于激进, 为了避免可能的漏判肿瘤导致的严重后果, 可以降低阈值, 这会提高recall
我们可以将阈值-recall, precision画成表, 曲线的形状根据数据不同会有不同
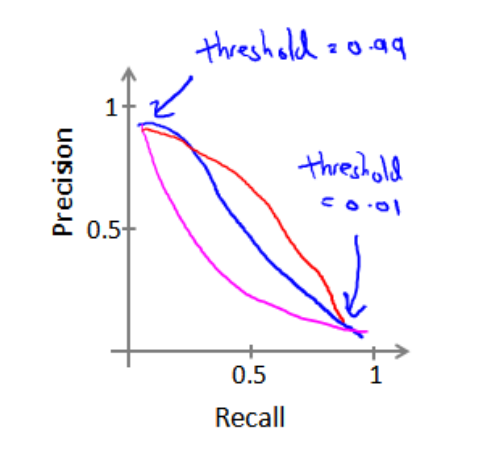
这里有一个可以帮助我们选择阈值的方法, F1 score
F_1Score=\frac{2PR}{P+R}
选择使得F1值最高的阈值比较合理
