还有一个更加强大的算法广泛的应用于工业界和学术界,它被称为支持向量机(Support Vector Machine)。
与逻辑回归和神经网络相比,支持向量机,或者简称 SVM,在学习复杂的非线性方程时提供了一种更为清晰,更加强大的方式。
优化目标
这里我们从逻辑回归开始, 一点点修改得到支持向量机
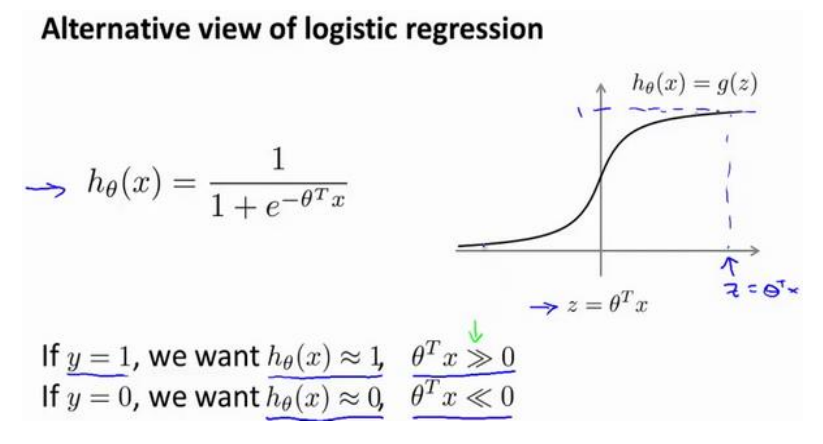
在逻辑回归中, 对于一个y=1的样本, 我们希望h(x)趋近于1, 那就要令 z = thetaX远大于0, 相对的, 如果对于y=0的样本, 我们希望z远小于0
支持向量机的损失函数可以在逻辑回归的损失函数上做如下修改:
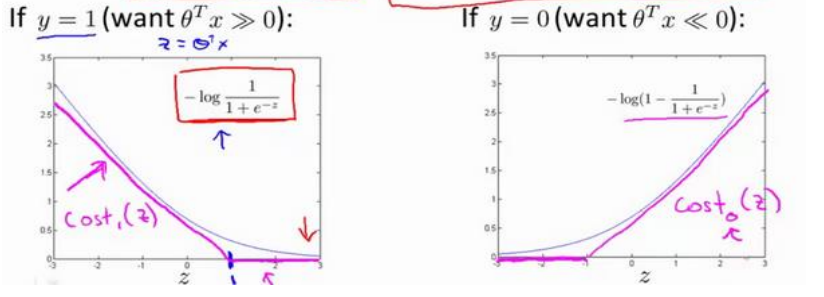
黑色的是逻辑回归的, 紫色的是支持向量机的
和逻辑回归一样, 需要对样本y值做分类讨论, 紫色图像是分段的直线, 且过(1, 0) 或者(-1, 0)
我们给两个新函数起名cost_0(z)和cost_1(z), 分别对应y=0和1的情况
支持向量机的整体损失函数可以由逻辑回归的函数如此修改得到
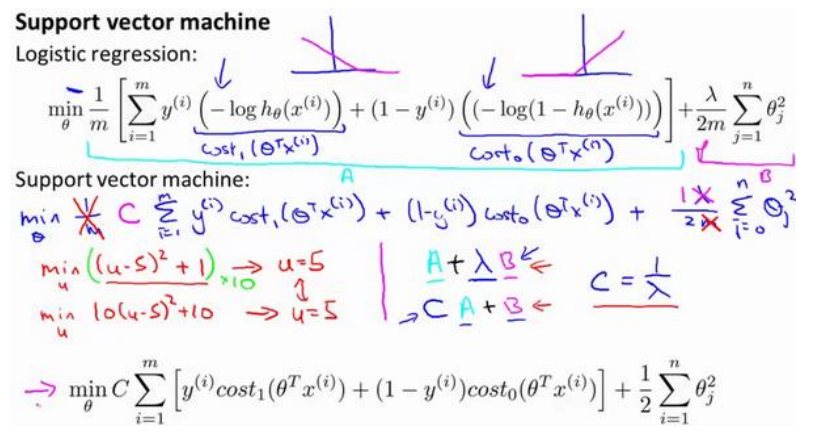
首先我们去掉了开头的常数1/m, 在逻辑回归中, 这代表着损失对每个样本的平均, 他是常数, 对整体的参数最小值取值没有影响, 去掉他是支持向量机的习惯, 没有绝对对错
然后用新的损失函数替代逻辑回归的
在支持向量机中, 用于平衡损失函数和正则化项的参数是C, 卸载损失函数前, 事实上可以看作扮演类似\frac{1}{\lambda}的角色
支持向量机的预测规则如下 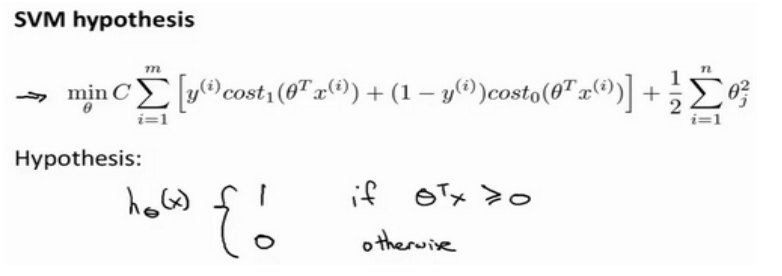
有别于逻辑回归输出概率, 支持向量机直接输出预测的结果
大边界(Large Margin)的直观理解
支持向量机也被称作大间距分类器, 通过理解"大间距"的由来, 有助于我们理解其思想

这里将0替换成±1是为了帮助模型更好的训练, 也可以叫做安全因子, 引导他做出明确的决定, 而非模棱两可的
我们看一下这个因子导致了什么结果: 具体而言, 考虑一个特例: 我们将C设置为一个非常大的数, 比如1e5, 来观察SVM的反应

因为C非常大, SVM会迫切的希望优化损失函数, 而非后面的正则化项, 我们假设可以优化其为0, 则, 对于一个y=1的样本, 我们需要z>=1, 反之则需要z<=-1
此时问题变成了, 令z在满足上述条件下, 优化正则项至最小(条件极值问题)
考察下面的二分类数据集:
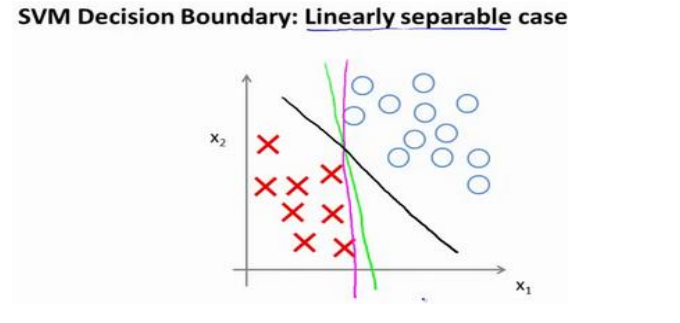
我们可以看到, 有很多决策边界可以将数据集分为两类, 但是SVM会选择黑色的一条, 看上去更加合理, 这是因为黑色直线离两侧数据都较远, 而决策边界到数据的距离就叫做间距(Margin), 下图中画出的部分
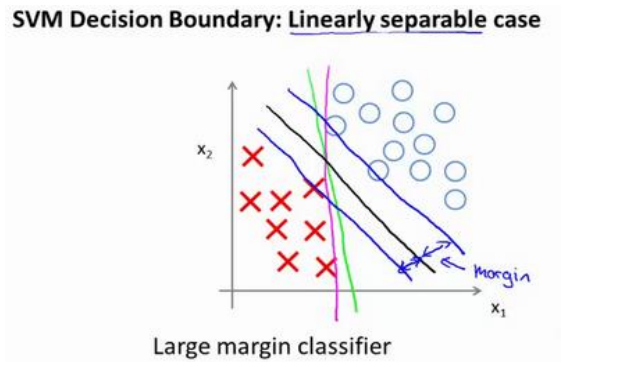
事实上我们的优化问题是
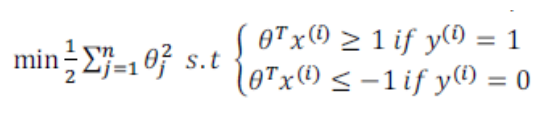
上图中s.t.是subject to的缩写, 意为受限于
这里需要注意一点, 常数C并不是越大越好, 考察下面的数据集, 注意数据集中的异常点(Outlier)

如果我们将C设置的过大, 比如1e5, 因为算法迫切的需要让第一项为0, 所以会画出粉色的决策边界, 这显然是不理智的
在实际应用中, 显然应该调整C的大小到合适, 以获得黑色的决策边界, 即, 当C不是非常大的时候, 算法可以忽略掉一些异常点的影响, 得到更好的决策边界
回顾C = 1/lambda, 因此

