无监督学习
从这节开始, 我们开始介绍无监督学习算法, 即, 让计算机学习无标签的数据, 而不是此前有标签的
无监督学习的数据看起来是这样的
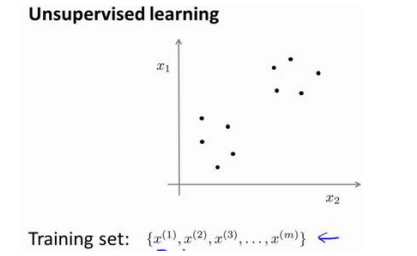
相比于之前的数据少了标签(y, 点的形状, 叉或者圈), 我们需要算法来告诉我们数据的结构
图上数据看起来可以分为两个分开的点集, 或者说簇(Cluster), 一个能找到这两个点集的算法就称作聚类算法
K均值(Kmeans)聚类算法是无监督学习的一个典型例子
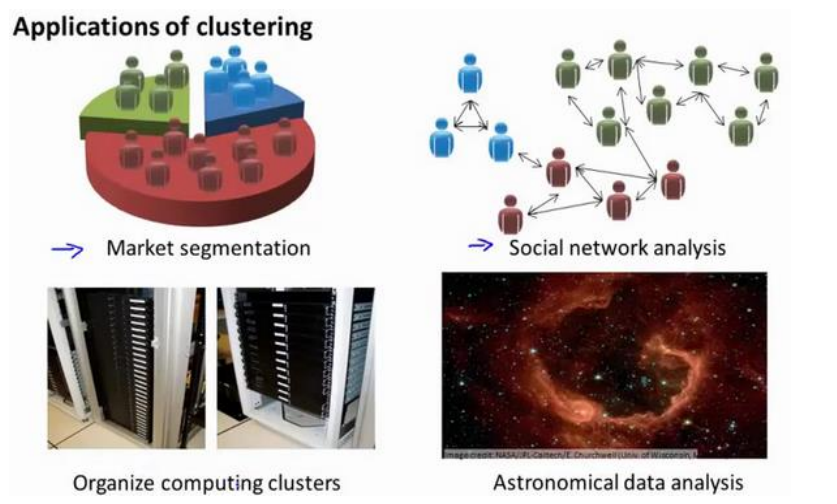
聚类算法有很多的应用场景, 比如给出大量客户的行为信息, 做出分类以便制定不同销售策略; 又如分析天体系统, 等等
K-means算法的思想
Kmeans是一个迭代算法, 假设我们现在要把数据分为K个组(K的选择方法后面会讲到), 比如下图中, 我们将选择K=3
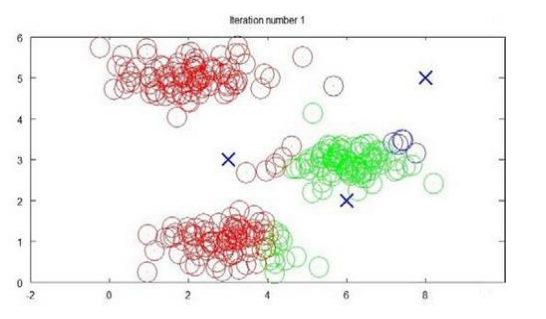
- 选择K个随机的点, 称为聚类中心(Cluster centroids)
- 对于数据集中的每一个数据, 选择其距离最近的聚类中心代表的类别
- 对于每一个聚类中心, 计算所属其的点的坐标平均值, 然后将中心移动到该位置
- 重复上面两步直到中心不再变化
下面是一个聚类示例:
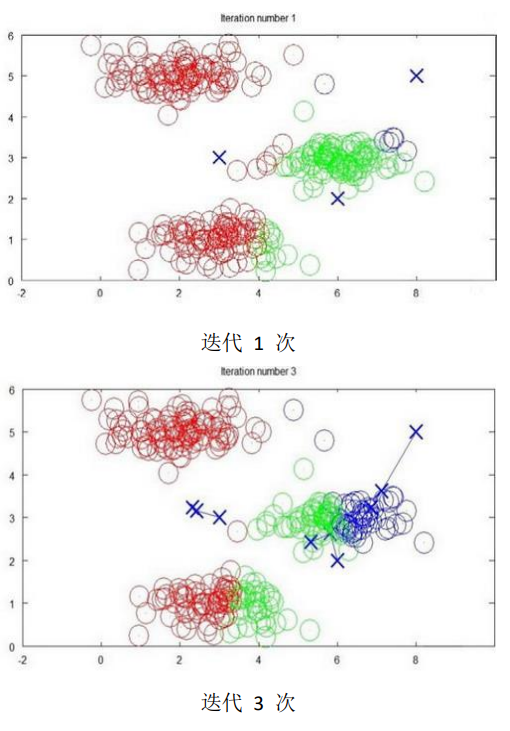
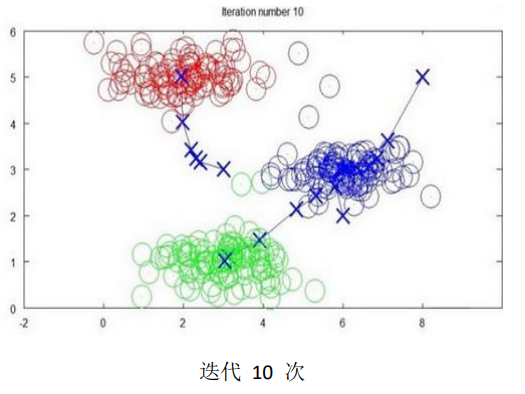
随着迭代, 聚类中心会渐渐走到类别的中心

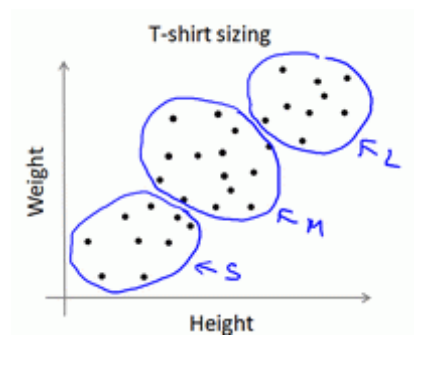
即使数据没有明显区分的时候, Kmeans也能将之分为不同的组, 下图所示的数据包含身高和体重, 以及Kmeans对数据的分类, 用以帮助确定衬衫尺寸
优化目标
Kmeans需要最小化的目标, 即是所有数据点和其所关联的聚类中心的距离之和, 因此Kmeans的代价函数(又称畸变函数, Distortion function)为
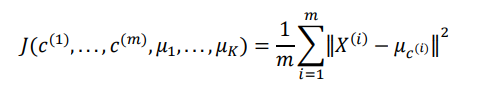
其中mui代表与x最近的聚类中心
回顾刚刚给出的迭代过程

第一个循环是用于减少ci引起的代价, 第二个减少mui_i引起的代价, 每一次迭代都在减小代价函数
随机初始化
Kmeans有一个问题: 算法有可能会停留在一个局部的最小值, 这取决于初始化聚类中心的情况
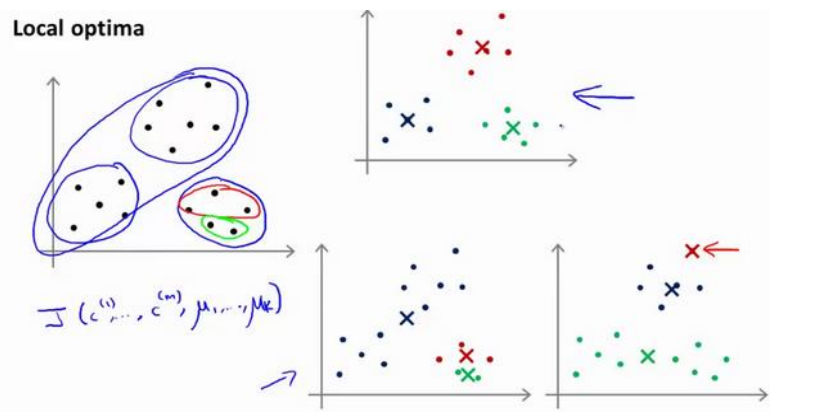
上图列出了几种可能的收敛结果, 只有一种是我们比较满意的
为了解决这个问题, 通常需要多次运行Kmeans, 每一次都重新随机初始化, 然后再比较多次运行的结果, 选择代价函数最小的结果, 这种做法再K较小时(2-10)是可行的, 如果K过大, 可能不会有明显的改善
选择聚类数(K)
事实上没有非常好的选择聚类数的方法, 通常是根据不同的问题进行人工选择
比如再衬衫分类例子中, 如果我们决定制造三个尺寸SML, 则就应当把客户分为三类, 又比如要制造五个尺寸, 多了XS和XL, 就分为五类
对于不明确要选择聚类数的情况, 这里有一个肘部法则可以用到
我们改变K值, 列出其对代价函数J的图像, 观察左图
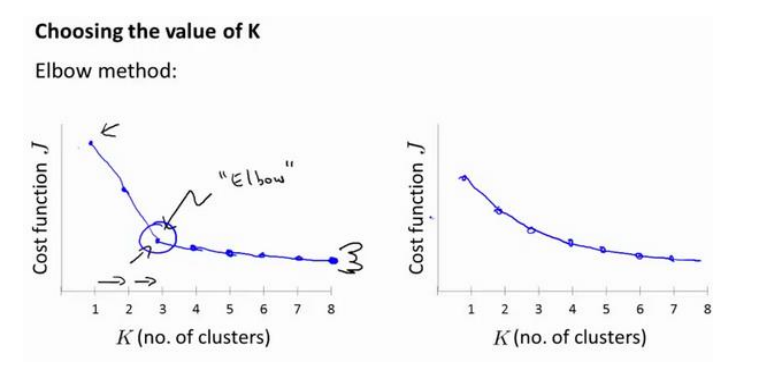
在K=3时, 有一个比较明显的拐点, 好像肘关节, 这表明使用K=3是比较合适的
当然在实际问题中, 不会永远都有这么理想的肘部可供选择, 时常遇到右图这样J均匀下降的情况, 这时还是需要根据实际需要来决定K的值
