这节谈一下降维问题(Dimensionality Reduction)
动机1: 数据压缩
通常来说, 我们收集到的数据集有很多特征, 这里挑选其中两个画在这里
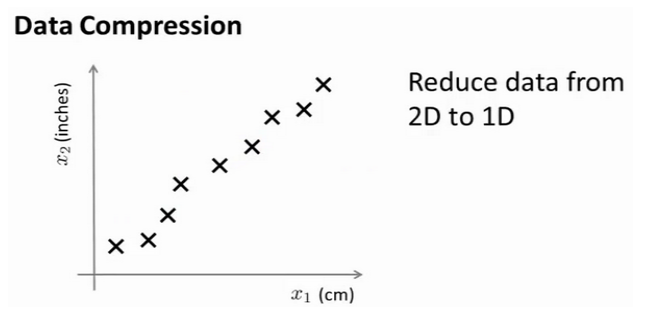
两个特征分别是长度(cm)和长度(inch), 当然因为测量误差, 四舍五入等原因, 点不一定在精确的一条直线上
事实上我们知道这两个特征相关度非常大, 以至于可以舍弃其中一个
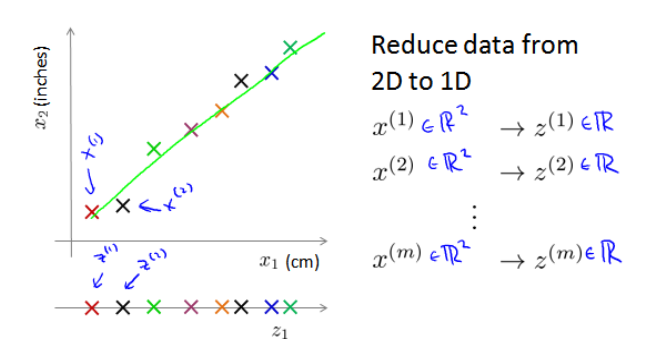
以上是二维到一维的降维, 也可以从三维到二维
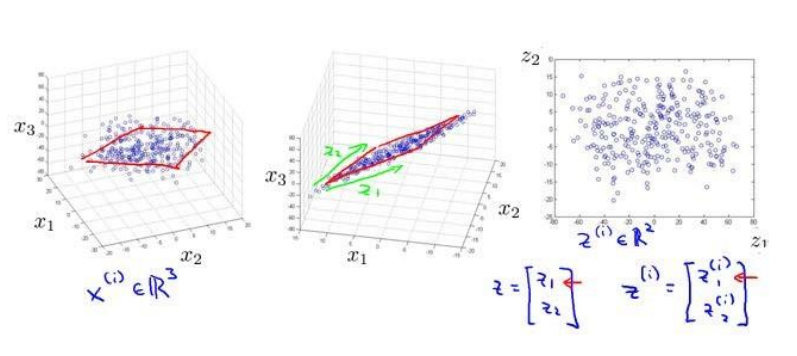
压缩数据可以节省内存空间, 加快模型运算效率等
动机2: 数据可视
在很多问题中, 如果我们可以将数据可视化, 就方便找到一个较好的解决方案
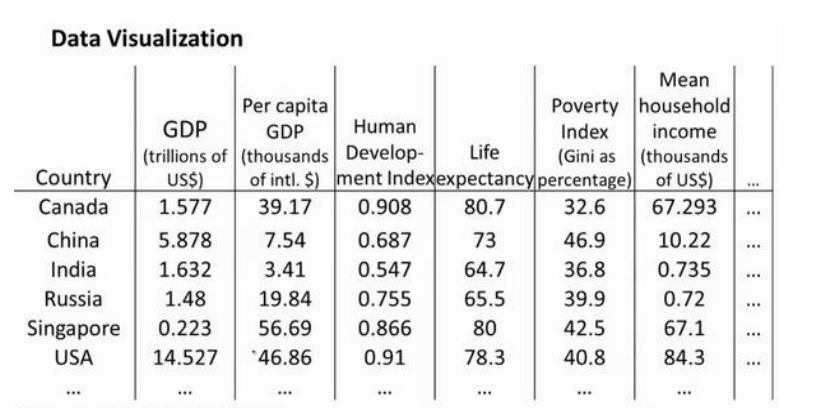
假设我们有许多不同国家数据, 每一个特征向量都是50维的, 如总GDP, 人均GDP, 平均寿命等. 要将其全部可视化是不可能的, 如果可以降至二维, 便可以看到
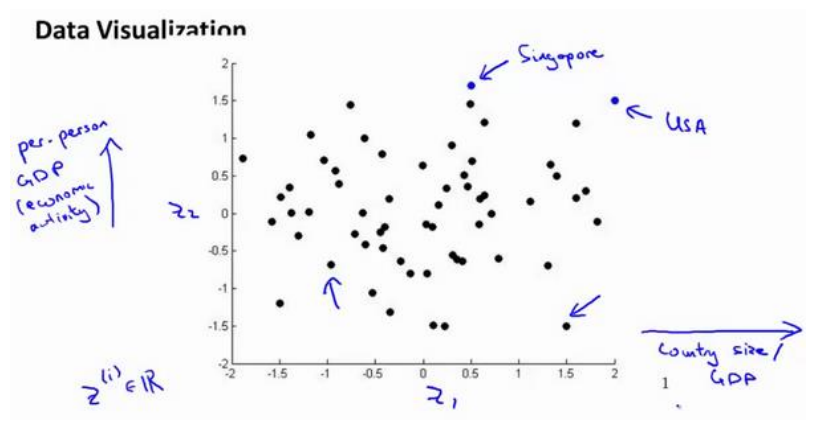
然而问题在于, 降维只负责减少维数, 新产生特征的意义必须由我们自己发现
主成分分析算法(PCA)
PCA是最常见的降维算法之一
在PCA中, 我们希望找到一个方向向量, 使得当我们把所有数据投影到其上时, 投影平均均方差最小
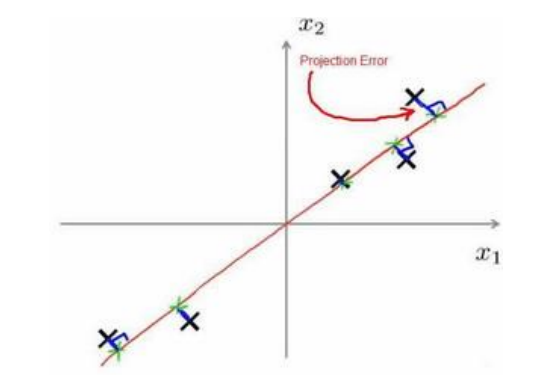
上图画出了投影误差的定义, 实际上就是到这个直线的距离
这里很多人会觉得和线性回归很像, 实则不然
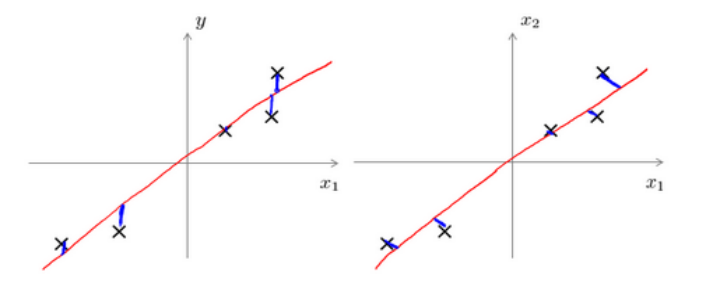
线性回归最小化的是拟合误差(左图), PCA最小化的是投影误差(Projected error)(右图)
PCA的优点在于无参数限制, 即, 在计算过程中不需要人为的设定参数或者干预, 最后的结果只和数据有关
这点也可以看作缺点, 如果使用者对PCA对象有一定的先验知识, 但却无法干预算法进程, 可能会得不到预期的效果
PCA的过程
第一步: 均值归一化, 计算出所有特征的均值, 然后向特征做差, 如果特征在不同量级上, 还需要除以标准差的平方
第二步: 计算协方差矩阵(Covariance matrix)
协方差矩阵写作大写的sigma, 看起来和求和符合完全一致, 计算方法如下
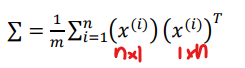
下面用红笔写出了矩阵形状, 所以协方差矩阵是n×n的
第三步: 求解协方差矩阵的特征向量(eigenvectors)
在octave里可以用奇异值分解(singular value decomposition, SVD)来求解
[U, S, D] = svd(sigma)对于一个size为[n, n]的矩阵, 上面的U是一个具有与数据之间最小投射误差的方向向量构成的矩阵, 当我们希望将数据压缩至k维时, 就取U中的前k个向量, 获得一个size为[n, k]的矩阵, 记为U_reduce
新的特征向量为
z^{(i)}=U^T_{reduce} *x^{(i)}
x的size是[n, 1], 所以结果size是[k, 1]
选择k的值
PCA的主要优化对象是均方差
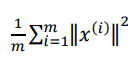
我们希望均方差与训练集方差的比例尽可能小的前提下, 让k尽可能小
如果这个比例小于1%, 则意味着原有数据被保留了99%
一种方法是分别令k=1, 2, 3, …以此类推, 直到我们找到一个满足保留率的k值
但是更好的方法是分析调用svd函数得到的3个参数U, S, V
S是一个[n, n]对角矩阵, 可以用它计算均方差和训练集的比例:
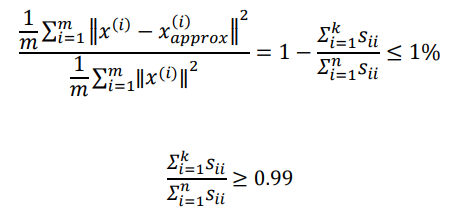
数据解压
PCA将高维数据压缩到低维, 如果要将低维数据还原, 总是有损失的
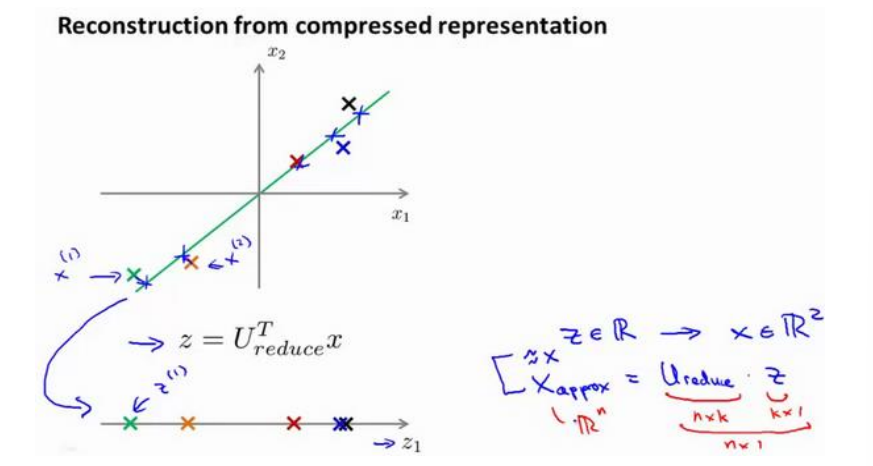
如图, 解压后的数据只能是原数据在低维的投影
压缩的公式是
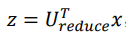
解压公式就是
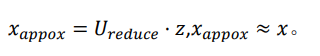
PCA的应用建议
在降维过程中, 不可避免的会造成信息丢失, PCA并不是百利而无一害的
第一条: 不要一开始就考虑用PCA, 先试试不用PCA实现目的, 如果遇到内存瓶颈或者效率不高时再考虑
第二条: 不要尝试用PCA解决过拟合问题, 即使PCA可以带来维度下降, 对防止过拟合有好处, 甚至可能会效果不错, 但是防止过拟合不是一个应用PCA的动机
