考察下面的分类问题
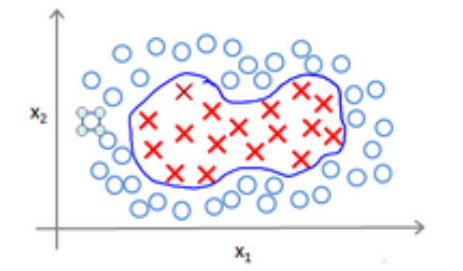
为了得到上图的决策边界, 一个可能的模型是
h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1x_2+\theta_4x_1^2+...如此这样的形式
我们可以用一系列新的特征f来替换模型中的每一项, 使得模型为
h_\theta(x)=\sum \theta_if_i的形式
然而, 除了对原有特征进行线性组合以外, 我们还可以用核函数(Kernel)来计算新的特征f, 这些f会优于上面的效果
对于一个给定的实例x, 我们选定了三个地标(Landmark)l1, l2, l3
事实上, 地标的位置和训练样本的位置一一对应, 具体的理由会放在下面
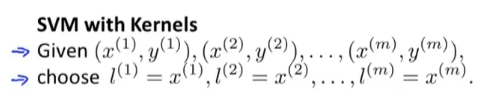
我们利用x的各个特征与地标的近似程度来生成新的特征f
f_i=similarity(x, l^{(i)})其中
similarity(x, y)=exp(-\frac{||x-y||^2}{2\sigma^2})
注意分子上面是向量的欧几里得距离, 就是几何距离
这里的similarity就是核函数, 具体而言, 这是一个高斯核函数(Gaussian Kernel)
这个核函数和正态分布没什么关系, 只是看上去像而已
这些地标的作用是, 如果训练实例x与地标L之间的距离近似与0, 则新特征f近似于exp(0)=1, 反之如果较远, 则f近似于exp(-INF)=0
对于高斯核中sigma的作用, 可以看下图
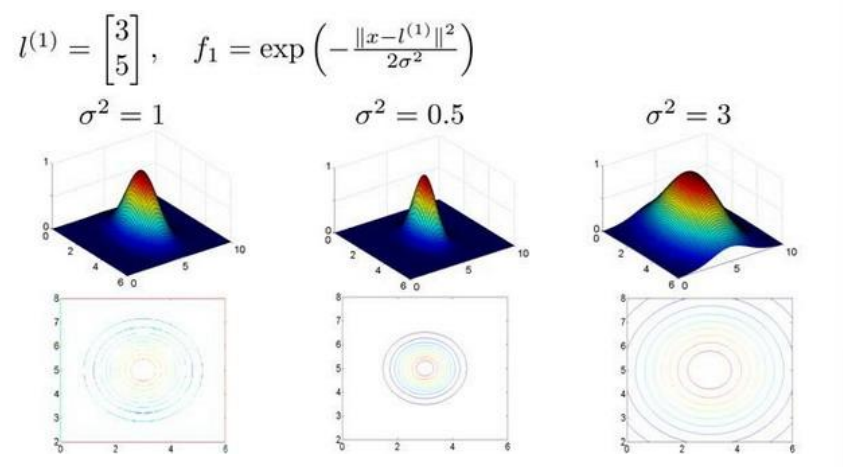
我们在实例中加入一个粉色的点x, 观察他的预测函数, 假设我们已经得到了theta的值, 分别是-0.5, 1, 1, 0

x离l1比较近, 离l2, l3较远, 所以f1接近1, f2, f3接近0, 此时结合theta的值, 可以计算得到h>0, 所以我们判定x属于该分类
事实上, 观察theta可以发现, 这个模型的意思是, 对于接近l1和l2的点, 我们更有可能将其判定为正, 而远离之的点更有可能被判定为负
这里的红色曲线是我们依据一个单一的训练实例和我们选取的地标得到的判定边界, 在预测时, 我们采用的特征不是训练实例本身的特征xi, 而是通过核函数计算得到的新特征fi
如何选择地标? 我们通常根据训练集的数量选择地标数量, 并且让地标与训练集数据一一对应
l^{(i)}=x^{(i)}, i \in [1, m]这样的好处在于, 我们得到的新特征是建立在原有特征与巡礼那几中所有其他特征距离基础上的, 即
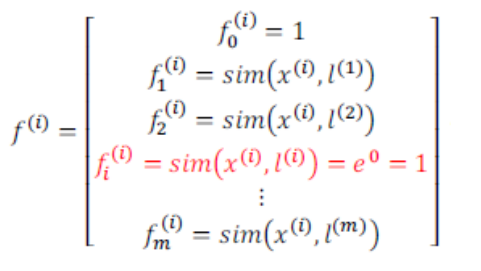
则支持向量机做出假设的过程如下

给定一个输入x, 计算新特征f, 然后根据theta计算z, 当z>=0时预测1, 反之预测0
在正则化项中, 我们可以用向量化的表达
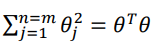
在实际应用中, 我们会调整成
\theta^TM\theta的形式, M是根据核函数选择的一个矩阵, 可以简化计算
理论上来说, 逻辑回归中也可以使用核函数, 但是上面用M矩阵简化运算的方法却不适用逻辑回归, 因此计算非常耗时
在此, 不介绍最小化支持向量机代价函数的方法
