为什么是神经网络
前几章讨论了线性回归和逻辑回归两种算法，他们都适合解决与线性函数相关的问题，而不擅长解决非线性的问题
下面是一个例子
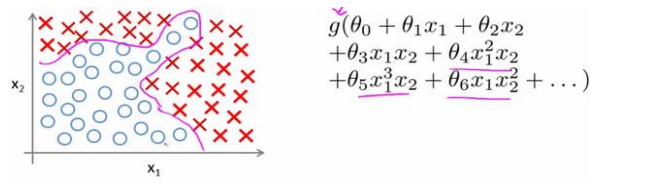
在如图的分类问题中，决策边界可能会非常复杂，这是只有两个特征x1,x2的情况，如果我们要用逻辑回归，就不得不用图中右侧非常复杂的函数，对多个参数进行回归
在实际情况中，特征可能非常多，比如在计算机视觉的例子中，我们要识别一张50×50的灰度图像内容，此时我们就有2500个原始特征，而即使只考虑他们之间的二元组合（二次项），也会有接近300万个特征，这不是普通的逻辑回归模型可以处理的特征量，事实上，这种问题需要神经网络
什么是神经网络
神经网络建立在很多神经元（也叫激活单元，activation unit）上，每一个神经元都是一个学习模型，下图是一个逻辑回归的神经元的例子
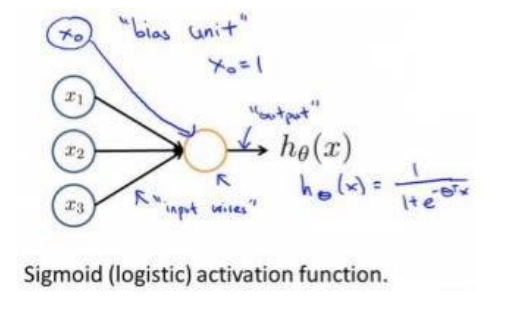
这个神经元有4个输入，一个输出，回忆逻辑回归的部分，x0总是等于1的（用来和theta0相乘得到函数的常数项），这里叫做偏置项(bias unit)，有时会省略不画
学习参数theta，在这里也叫权重（weight），经常写到输入端到神经元的连线上
现在观察下图的神经网络例子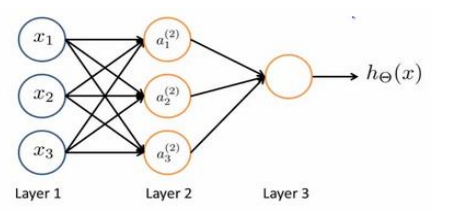 
最左侧是三个输入单元（input units），用来接收原始数据，中间的a是中间单元，负责数据处理，然后输出单元负责计算和输出
这三层分别称作输入层，隐藏层，输出层
现在加上偏置单元再来看一下
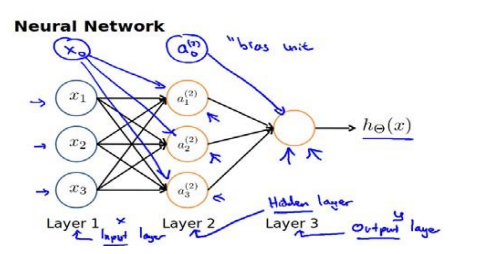
新加的两个偏置单元总是等于1的，所以注意x不会影响到a02的值
下面引入一些标记法来帮助描述模型
a_i^{(j)}表示第j层的第i个激活单元（神经元），\theta^{(j)}表示第j层到第j+1层的权重（参数）矩阵，他的形状应该是以j+1层神经元数量为行数，以j层神经元数位列数的，如上图\theta^{(1)}的尺寸就是3×4
对于上图的模型，隐藏层和输出层的表达式是
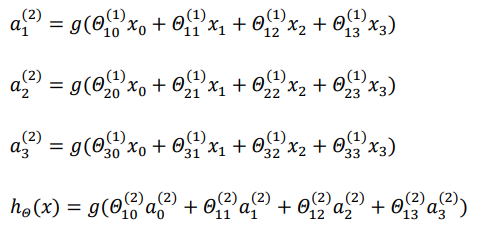
用向量化来表达
这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION )
这只是针对训练集中一个训练实例所进行的计算。如果我们要对整个训练集进行计算，我们需要将训练集特征矩阵进行转置，使得同一个实例的特征都在同一列里。即
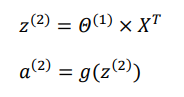
为了更好的理解神经网络，我们把上图遮住一部分
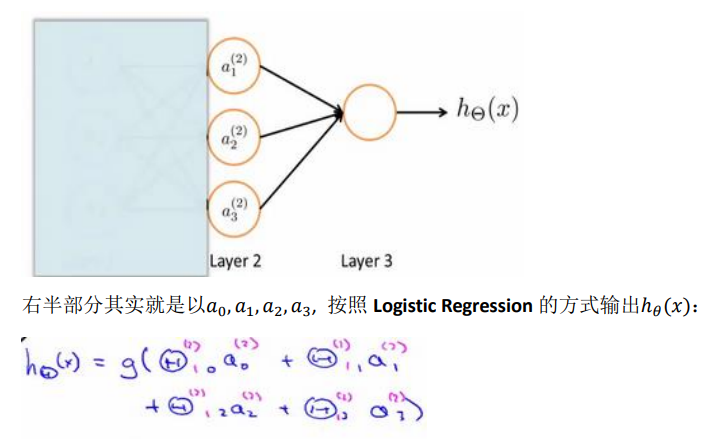
其实神经网络与逻辑回归有很多相似支持，只不过在神经网络中，我们不再像逻辑回归那样使用原始特征训练，而是使用前半部分模型训练过的值，这可以看作是更高级的特征值，即a是x的进化体，作为特征值来说，比x的线性组合要更加有效
这就是神经网络相比于逻辑回归和线性回归的优势
几个逻辑运算的例子
下面给出几个逻辑运算神经元的例子，如下图是and运算的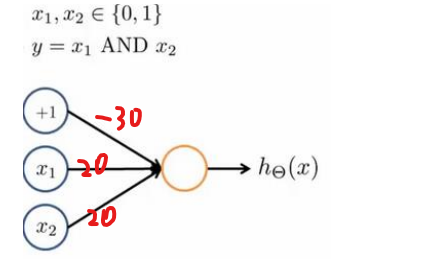 
结合g(x)的函数图像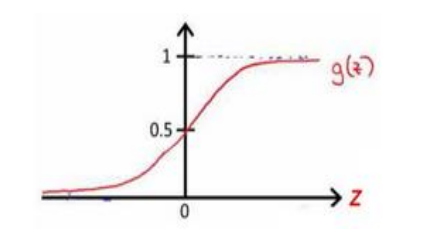 
我们可以写出真值表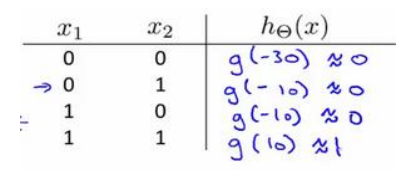 
可以看到神经元模拟了and函数的功能
神经元可以互相组合来实现复杂的逻辑运算，比如XNOR
因为
XNOR=(x1 AND x2)OR((NOT x1)AND(NOT x2))所以可以
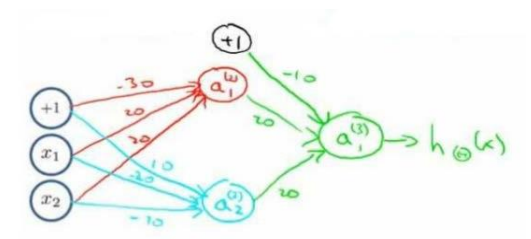
上图就是一个实现XNOR运算的神经网络
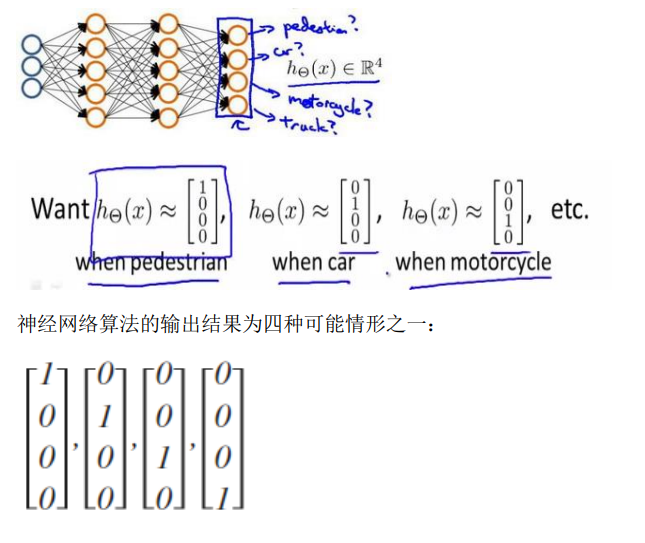
多分类问题
当我们有不止两种分类时，例如我们要对一个图片做出行人，汽车，摩托车或卡车的四分类问题，我们需要如下方法
