代价函数
首先做出一些约定，以方便后面讨论
我们假设神经网络的训练样本有m个，分别是(x^{(i)}, y^{(i)})L表示神经网络的层数 S_l表示第l层的神经元个数，自然的，S_L表示输出层的神经元个数
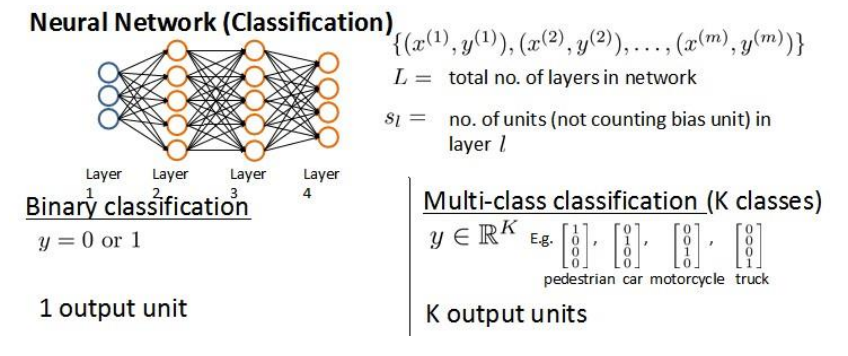
神经网络的分类有两种情况，二元分类和多元分类，注意下图在多分类中使用的的One-Hot编码
现在复习一下逻辑回归的代价函数
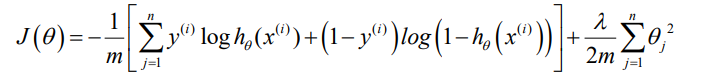
在逻辑回归中，x和y都是标量，但是在神经网络中，x是向量，维度是特征数量，h_\theta(x)是K维向量，K是分类数目，因此
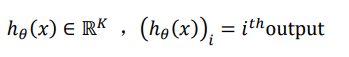
后者是我们做的约定
所以神经网络的代价函数是
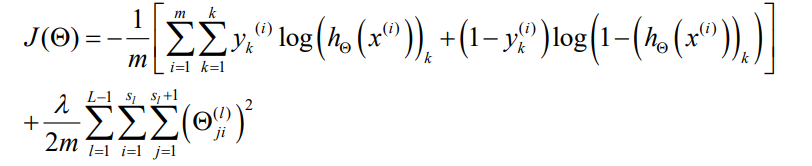注意图中求和的第三层应该改成s_(l+1)，原因下面会解释
先说前半部分的变化，比原先多了从k=1到k的求和，代表对于每一个组数据（x,y）（m是在枚举所有测试数据），都需要对所有输出节点产生的误差求和，注意k是分类数目，自然也是输出层的节点数目
再说后面正则化的部分，这里实际上还是对每一层除了\theta_0以外的参数正则化
首先l枚举层数，根据参数矩阵的定义，\theta^{(l)}表示从l层到l+1层的参数矩阵，自然输出层向后的参数矩阵，l的范围是1到L-1
然后ij枚举参数矩阵的元素，看一下下面这张图，代表第l层的网络情况
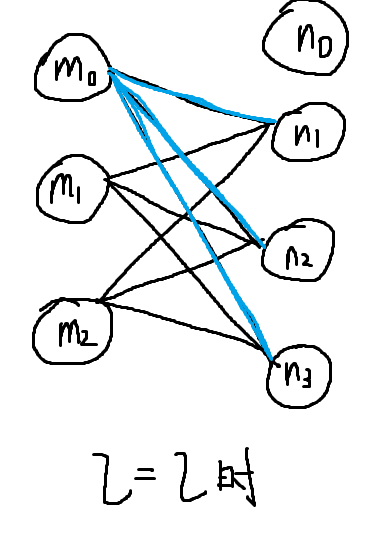
首先注意，参数矩阵的编码方式是从终点到起点，比如m1到n2的边是theta[2][1]，这是为了方便向量化，看如下图
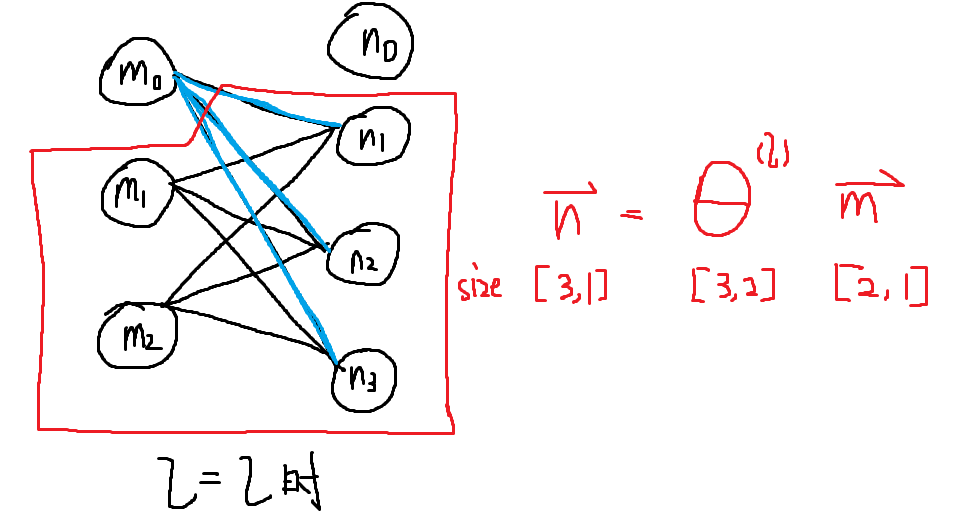
红色部分是忽略偏置后的结果，实际上不忽略也不影响结果
根据惯例，偏执单元(m0)的出边边权，即蓝色部分不参与正则化，所以theta[0][i]不参与正则化。
而前一级节点没有到下一级偏执单元节点的出边（偏置单元总是为1的，他不会更新，自然不用接受参数），所以theta[i][0]不参与正则化
根据theta矩阵的形状定义，自然有i从1到sl，即m层节点数目,而j是1到s(l+1)，即n层节点数目
反向传播
啰嗦这么久，终于可以进入正文了，反向传播是神经网络用来更新参数矩阵，以此最小化代价函数的算法，他的进程几乎是正向传播的逆序
要最小化代价函数，我们需要知道代价函数对每个参数的偏导数，以此来实行梯度下降或其他高级的优化法，即
\frac{\partial}{\partial \Theta ^{(l)}_{ij}} J(\Theta)现在假设我们的训练集只有一组数据(x, y)，在图中的神经网络中，前向传播的执行是这样的
注意上图中用的是向量化的表达
我们用\delta^{(i)}来表示每一层的误差，显然在输出层中,即，l=L时
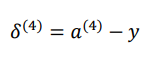
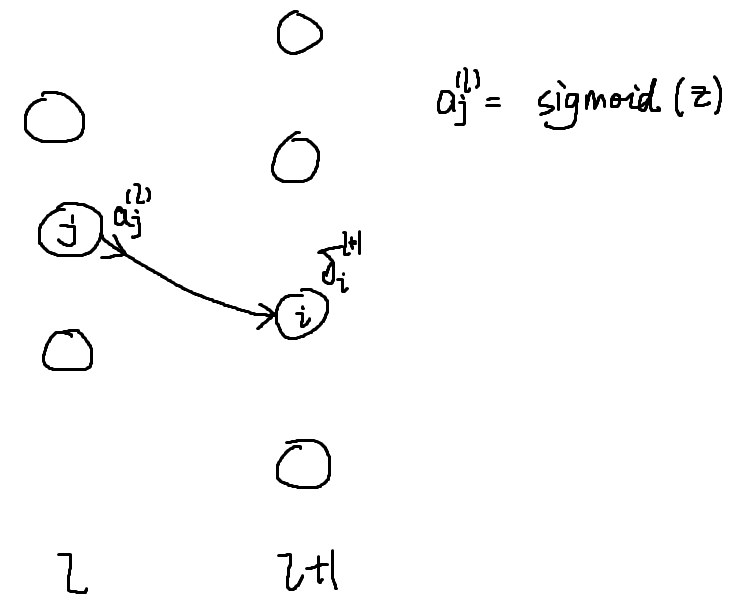
我们用这一层的误差反向转播至前一层，来推算前一层的误差
\delta ^{(i)}=(\Theta^{(i)})^T\delta ^{(i+1)}*g'(z^{(i)}) , i=1,2,...,L-1这里的星号是点乘的意思
在上式中
g'(z^{(i)}) =a^{(i)}(1-a^{(i)})这是因为g是sigmoid函数
g(x) = \frac{1}{1+e^{-x}}
\\
g'(x) = g(x)(1-g(x))sigmoid函数的求导非常常用，需要特别记忆一下，否则就会和我一样，别人一步过的步骤问半天（orz）
在我们更新完成所有的delta表达式后，便可以计算代价函数的偏导数了，以下是不加正则化处理的情况
\frac{\partial}{\partial \Theta ^{(l)}_{ij}} J(\Theta)=a_j^{(l)}\delta_i^{l+1}这里推导比较复杂，看了个半懂不懂，抽时间专门写一篇博客，现在暂时先往后进行，毕竟步步追求严谨的证明是很影响学习效率的（逃）
画个图直观的看一下，可以看到反向传播在逆向的传播误差
现在推广到一般情况，我们考虑正则化处理，并且我们的训练集是一个矩阵，此时的误差单元也是一个矩阵，我们用\Delta_{ij}^{(l)}表示第l层第i个神经元受到第j个参数影响的误差,即第l层ij这条边的误差 算法表示如下
即首先用正向传播方法计算出每一层的激活单元，利用训练集的结果与神经网络预测的结果求出最后一层的误差，然后利用该误差运用反向传播法计算出直至第二层的所有误差
然后用下面方法计算D，按照是否有正则化来讨论，当j=0时，按照惯例不正则化（蓝色线）
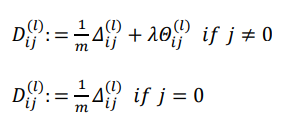
可以证明
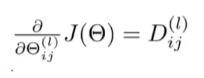
证明很复杂，这里不写了，有时间专门研究一下
这节难度略大，借用吴恩达老师的话说，大部分人在第一次接触反向传播算法时都会感到困惑，它不像线性回归或者逻辑回归那样"mathematical clear"，这是完全正常的，即使是很多研究人员，在应用反向传播算法达成很多目的后，也不完全清楚他的完整原理（权当谦虚）
下一节将会介绍对反向传播算法的感性理解和一些在实施算法过程中的注意事项