梯度检验
反向传播算法的实现过程比较复杂,容易产生小错误,并且这些小错误有时并不明显——从小数据的结果来看,并没有严重影响结果,这是非常致命的,因为错误会随着数据增多变得更加明显,但我们再调试的时候却往往不能定位他的具体位置
为了避免这种问题,我们采取数值梯度检验(Numerical Gradient Checking)方法来检测我们的偏导是否计算正确
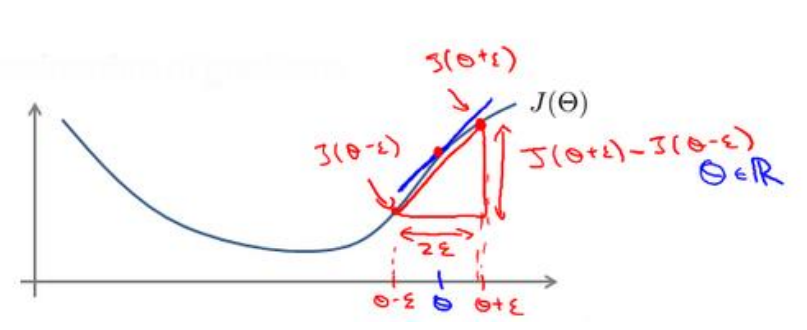
即对于某个特定的 𝜃,我们计算出在 𝜃-𝜀 处和 𝜃+𝜀 的代价值(𝜀是一个非常小的值,通常选取1e-5左右),然后求两个代价的平均,用以估计在 𝜃处的代价值
这种方法是双侧估算,当然也可以只对一个方向估算,不过双侧的方法精度稍好一些
下面是针对一个theta1的检验
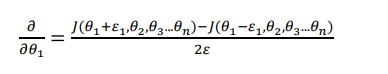
随机初始化
任何优化算法都需要初始参数,有人会觉得所有初始参数都是0是可行的,但这只对逻辑回归可行,对神经网络不可行,因为当我们将所有参数置零,这意味着第二层的所有神经元都是相同的值,最后一层也是,然后在反向传播时候,delta也都变成一样的,事实上,如果我们将所有参数都初始化为同一个非零的数,结果也一样
我们通常随机初始化参数在正负epsilon范围内,比如我们需要随机初始化一个10×11的矩阵,代码是
Theta1 = rand(10, 11) * (2*eps) – eps
总结一下
小结一下使用神经网络时的步骤:
- 网络结构:第一件要做的事是选择网络结构,即决定选择多少层以及决定每层分别有多少个单元。
- 第一层的单元数即我们训练集的特征数量。
- 最后一层的单元数是我们训练集的结果的类的数量。
- 如果隐藏层数大于 1,确保每个隐藏层的单元个数相同,通常情况下隐藏层单元的个数 越多越好。
训练网络的基本步骤

